Structures corresponding to long range

In this subsection, we consider those structures which become the global minimum only at low values of $\rho_0$.We have restricted our study to those clusters with $\rho_0\ge 3$, since we do not know of a case where longer-ranged potentials might be relevant. The low $\rho_0$ structures that we have found separate into two size ranges: those with N around 13 and those with N>45. The former set have been described in a previous paper,[38] but we illustrate them again in Fig. 15 because the connection to Kasper polyhedra[87,88] was not originally identified and because they are important for understanding the structures that occur at larger N.

The majority of the structures associated with low $\rho_0$ are polytetrahedral: the entire cluster can be divided into tetrahedra with atoms at the vertices. These minima also tend to be close to spherical in shape and highly strained in order to maximize n_nn. As we noted earlier, the 13-atom icosahedron is polytetrahedral. In this case, each nearest-neighbour contact between the centre and a vertex is the common edge of five tetrahedra. This is also true of all the nearest-neighbour contacts in the rhombic tricontahedron (45A) which do not lie on the surface. Nearest-neighbour contacts which are surrounded by more or less than five tetrahedra are said to have defects called disclination lines running along the interatom vector. Those contacts surrounded by more than five tetrahedra are termed negative disclinations (if there are six it is a $-72^\circ$ disclination, if there are seven a $-144^\circ$ disclination, ...) and those surrounded by fewer than five tetrahedra are termed positive disclinations (if there are four it is a $+72^\circ$ disclination and if there are three a $+144^\circ$ disclination).

Most of the structures associated with low $\rho_0$ are polytetrahedral and involve disclinations. Although packing five tetrahedra around a nearest-neighbour contact involves some strain, the energetic penalty associated with either more or less tetrahedra is greater. Therefore, structures involving disclinations are only likely to be lowest in energy for long-ranged potentials where the associated strain can be most easily accommodated, and where they must have a larger n_nn than the alternative disclination-free structures. A $-72^\circ$ disclination line involves less strain than a $+72^\circ$ disclination line because of the gap that remains when five regular tetrahedra share a common edge (Fig. 3(a)). Consequently, structures which involve only negative disclinations, or an excess of them, are more common amongst the low $\rho_0$ global minima.

To visualize the network of disclination lines in a structure, one must first partition space according to the Voronoi procedure, in which each point is assigned to the Voronoi polyhedron of the atom to which it is closest. This allows nearest neighbours to be defined as those atoms whose Voronoi polyhedra share a face. The Delaunay network that results from joining all such nearest neighbours is the dual of the Voronoi construction and divides all space into tetrahedra. This definition of a nearest neighbour has been termed geometric, rather than physical (e.g. using a cutoff distance), and the corresponding division of space into tetrahedra is artificial in the sense that it is independent of whether a polytetrahedral description is appropriate.

In practice we determined the Voronoi polyhedra from the fact that a set of four atoms constitutes a Delaunay tetrahedron if the sphere touching all four atoms contains no other atoms.[89] The centre of this sphere is then a vertex of the Voronoi polyhedron of each atom. As the number of tetrahedra around a nearest-neighbour contact is the same as the number of sides for the face common to the Voronoi polyhedra of both nearest neighbours, disclination lines can then be assigned. However, problems can occur in assigning the Delaunay network if there are more than four atoms exactly on the surface of the sphere. Such a degeneracy, which only occurs as a result of symmetry, renders the analysis non-unique. This is the case for the 55-atom Mackay icosahedron and for bulk close-packed solids because of the presence of octahedral interstices, but it is not a problem here since we only apply the method to clusters that are polytetrahedral in character. One further consideration is that the analysis should not be applied to nearest-neighbour contacts between the surface atoms of a cluster.

  

Figure 15: Low energy minima for small clusters at low values of $\rho_0$. If appropriate, the disclination network is displayed next to each structure. $-72^\circ$ disclinations are represented by red lines and $+72^\circ$ disclinations by blue lines. 17F and 20C are never global minima.

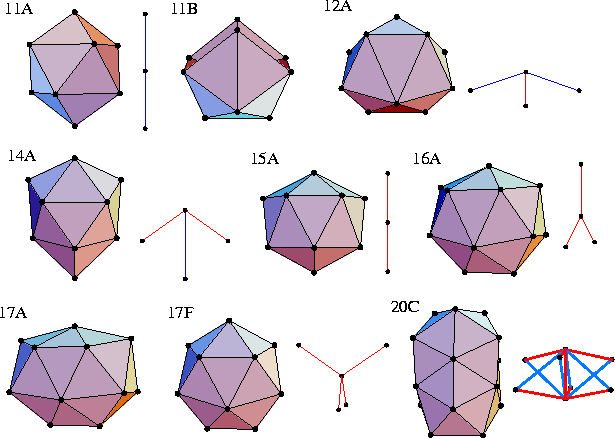The smallest global minimum that involves a disclination line is 11A where the central atom is surrounded by a 10-atom coordination shell. This encapsulation gives the structure a larger n_nn than the incomplete icosahedron (structure 11B of ref. [38]), but results in a larger strain energy.[38] The structure involves a single positive disclination line running through the centre of the cluster. Similarly, for N=12 and 14-16, clusters with a single coordination shell become lower in energy than structures based on the icosahedron at long range. Structures 11A, 12A, 14A, 15A, 16A and 17F (the second lowest energy structure of $\rm M_{17}$ at $\rho_0=3$)correspond to Kasper polyhedra. Of these structures 15A is the most stable in terms of the range of $\rho_0$ for which it is the global minimum.[38] The Kasper polyhedra are the deltahedral coordination shells that involve the minimum number of disclinations. They are important in the Frank-Kasper phases,[87,88] which are crystalline structures that are polytetrahedral and involve ordered arrays of negative disclination lines. Much interest has been focussed on the Frank-Kasper phases because they are closely related to icosahedral quasicrystals.[90] Indeed a recent three-dimensional model of quasicrystalline structure was based upon clusters involving disclination lines similar to those we find here.[91]

Structures 11A, 12A, 14A, 15A and 16A are all deltahedral, and so growth can occur in both `anti-Mackay' and `Mackay' sites (Fig. 7). However, if one considers the addition of a hexagonal pyramidal cap to the most stable of the Kasper polyhedra, 15A, the result is a D_6h structure with a positive disclination running the length of the symmetry axis (a disclinated equivalent of the double icosahedron 19A) which has only the same n_nn as the icosahedral structure 22A. Disclinated polytetrahedra cannot compete with the disclination-free polytetrahedral structures produced by an anti-Mackay overlayer on the icosahedron. Only once the latter growth sequence is completed at N=45 are structures with disclinations again global minima (Fig. 16). The one exception is structure 38A, which is similar to the icosahedral structures 38B and 38C, but has two positive disclinations running through the structure in a strange double helical twist.

Interestingly, structures with anti-Mackay growth on 11A have been recently observed for M⁺RG_N (M--metal, RG--rare gas) clusters where the metal ion is sufficiently small with respect to the rare gas atoms.[92] The metal ion presumably lies in the centre of the cluster, and the size ratio ensures that the cluster is least strained when the metal ion is surrounded by 10 rare gas atoms. Similarly, one might expect structures with negative disclinations to occur for AB_N clusters when A is sufficiently large with respect to B that a coordination number of larger than twelve is favoured for the A atom.

  

Figure 16: Global minima at low values of $\rho_0$ for $N\ge 38$.If appropriate, the disclination network is displayed next to each structure. $-72^\circ$ disclinations are represented by red lines, $+72^\circ$ disclinations by blue lines, $-144^\circ$ disclinations by green lines and $+144^\circ$ disclinations by yellow lines.

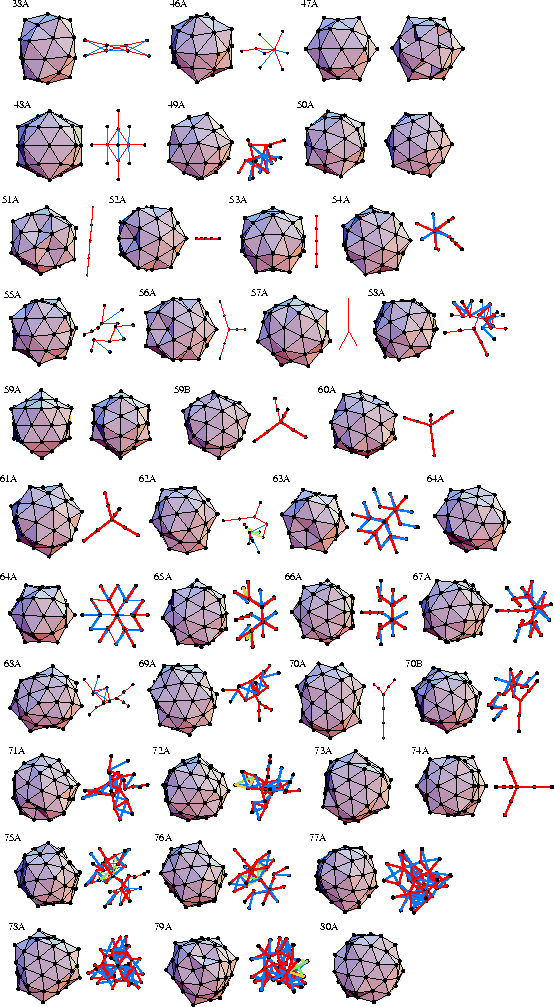The most stable disclinated polytetrahedral structures occur at N=53, 57, and 61 (Fig. 5(a)). These are the sizes for which complete `anti-Mackay' overlayers on 15A, 16A and 17F are possible. The effect of the overlayers is to extend the disclination lines emanating from the central atom. In these structures, those interior atoms not lying on a disclination line are icosahedrally coordinated. Many other minima are related to these stable structures: 51A and 52A are based on 53A but with missing vertex atoms; similarly, 59B and 60A are based on 61A; and 70A and 74A are based on 57A and 61A, respectively, but with an additional 13-atom cap which extends one of the `arms' of the disclination network. Furthermore, many of the other structures include parts of the disclination networks of 53A, 57A and 61A, but combined with a more disordered array of disclinations in another part of the cluster.

Other interesting structures are also seen. 47A, 50A and 59A seem to have a mixture of Mackay and anti-Mackay overlayers. 64A is formed from the rhombic tricontahedron 45A by the extension of the structure along a three-fold axis and the addition of a ring of atoms in the centre. In the middle of 64A is the D_3d structure 20D (the third lowest energy structure for $\rm M_{20}$ at $\rho_0$=3) which can be regarded as two highly strained interpenetrating icosahedra. However, for the larger clusters it becomes difficult to recognize any structural motifs, and some just seem to be disordered tangles of disclinations.

The above results are particularly interesting because of their relevance to our understanding of liquid structure. The minima described above, when reoptimized at larger values of $\rho_0$, correlate with structures which lie in the lower energy range of the band of minima associated with liquid-like clusters.[41,42] This is because simple liquids have significant polytetrahedral character,[93] as has been shown by the success of the dense random packing of hard spheres[94,95] as a model for metallic glasses[96] and later by computer simulations.[97] Indeed, Nelson has suggested that simple liquids are polytetrahedral packings that are characterized by a disordered arrangement of disclination lines.[98,99] Consequently, by examining the global minima associated with low $\rho_0$ we can study the size evolution of polytetrahedral packings, and the development of bulk liquid structure. At small sizes disclination-free polytetrahedra based on icosahedra with anti-Mackay overlayers are possible; at larger sizes polytetrahedra with ordered arrangements of disclinations are most common, and finally at the largest sizes in this study the polytetrahedra have a disordered disclination network. The latter geometries are structurally very similar to fragments of bulk liquid, except that the density of disclination lines is lower.[42]

Theoretical studies of sodium clusters have shown that amorphous structures are lower in energy than regular geometries up to at least 340 atoms, the largest size considered in that study.[100] The present results suggest that the these disordered structures are due to the relatively long range of the sodium interatomic potential. Amorphous structure for sodium is also suggested by the experimental observation of electronic shells[101] and supershells,[102] which are incompatible with any of the ordered morphologies one might expect.[103] Indeed, the transition from electronic to geometric magic numbers which occurs at about 1000 atoms[25] probably reflects a change in the lowest energy structures from amorphous minima to Mackay icosahedra, which can be explained by the twin effects of the size and the range of the potential.[41,42]

Since most minima associated with small values of $\rho_0$ do not have a common lattice or packing scheme, it is difficult to predict the low energy structures, and so most have been found by one of the global optimization methods. Fortunately, these methods are most likely to succeed for long range potentials because the corresponding PES's are smoother and support fewer minima than for shorter range. Another consequence of the lack of lattice structure is that the differentiation between nearest neighbours and next-nearest neighbours becomes ambiguous and the decomposition of eqn. (2) more arbitrary. For these clusters we chose to define n_nn using a cutoff at $\rho_0$=4 which corresponds to the distance at which the pair energy is $0.6\,\epsilon$.