 |
 |
The results are summarized in Fig. 4 which provides a zero temperature `phase diagram',
showing how the global minimum depends upon N and ![]() .
The structural behaviour of Morse clusters with fewer than eight atoms is rather uninteresting
because the global minimum is independent of
.
The structural behaviour of Morse clusters with fewer than eight atoms is rather uninteresting
because the global minimum is independent of ![]() .For all
.For all ![]() , however, the global minimum changes at least once as a function of
, however, the global minimum changes at least once as a function of ![]() .For
.For ![]() , icosahedral, decahedral and fcc structures all exist,
and the form of the phase diagram is in good agreement with the predictions we
made earlier based upon the decomposition of the potential energy.
For most sizes the structure changes from icosahedral to decahedral to close-packed as the
range of the potential is decreased.
For N<23, however, the transition from decahedral to close-packed occurs at larger values
of
, icosahedral, decahedral and fcc structures all exist,
and the form of the phase diagram is in good agreement with the predictions we
made earlier based upon the decomposition of the potential energy.
For most sizes the structure changes from icosahedral to decahedral to close-packed as the
range of the potential is decreased.
For N<23, however, the transition from decahedral to close-packed occurs at larger values
of ![]() than we consider in this study.
There are also a number of sizes (N=38-40, 52, 53, 59 and 61) for which there is
a transition directly from an icosahedral to a close-packed structure;
this occurs when nnn for the lowest energy close-packed structure is greater than
or equal to that for the lowest energy decahedron.
than we consider in this study.
There are also a number of sizes (N=38-40, 52, 53, 59 and 61) for which there is
a transition directly from an icosahedral to a close-packed structure;
this occurs when nnn for the lowest energy close-packed structure is greater than
or equal to that for the lowest energy decahedron.
The boundaries between the different morphologies are sensitive functions of N.
Such size dependence is observed for many properties of clusters, and gradually
lessens as N increases (because the addition of a single atom becomes a smaller
perturbation) until the bulk limit is reached.
The decahedral to close-packed boundary is particularly sensitive,
because the range of ![]() for which the decahedron is most stable changes dramatically even
when the difference in nnn between the decahedral and close-packed structures changes by one.
for which the decahedron is most stable changes dramatically even
when the difference in nnn between the decahedral and close-packed structures changes by one.
Sizes for which a morphology is the lowest in energy for a particularly large range of ![]() indicate that the structure is especially stable.
The optimal geometries shown in Fig. 1 are good examples.
Another indicator of special stability is provided by
indicate that the structure is especially stable.
The optimal geometries shown in Fig. 1 are good examples.
Another indicator of special stability is provided by ![]() .Peaks in
.Peaks in ![]() have been found to correlate well with the magic numbers (sizes at which clusters are
particularly abundant) observed in mass spectra.[71]
Plots of
have been found to correlate well with the magic numbers (sizes at which clusters are
particularly abundant) observed in mass spectra.[71]
Plots of ![]() are shown in Fig. 5 for a number of values of
are shown in Fig. 5 for a number of values of ![]() .
Unsurprisingly, the plot for
.
Unsurprisingly, the plot for ![]() =6 is very similar to that for LJ clusters with peaks
due to especially stable icosahedral clusters.
At higher values of
=6 is very similar to that for LJ clusters with peaks
due to especially stable icosahedral clusters.
At higher values of ![]() peaks corresponding to close-packed
and decahedral clusters begin to occur.
The plot at
peaks corresponding to close-packed
and decahedral clusters begin to occur.
The plot at ![]() =14 is very similar to that recently obtained for
=14 is very similar to that recently obtained for ![]() clusters using
the Girifalco intermolecular potential.[72]
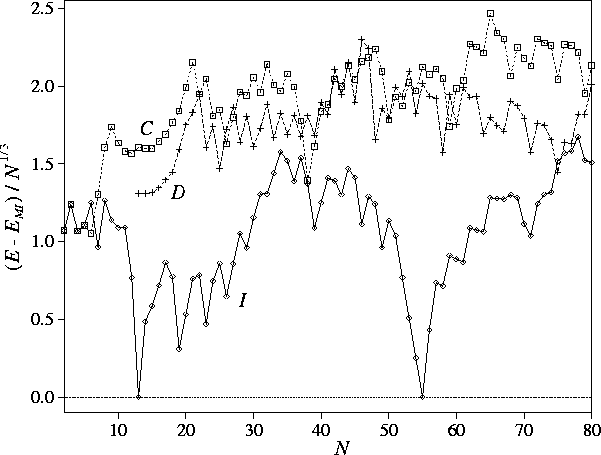
If the energy is `normalized' by subtracting a suitable function of N, particularly
stable sizes again stand out (Fig. 6).
clusters using
the Girifalco intermolecular potential.[72]
If the energy is `normalized' by subtracting a suitable function of N, particularly
stable sizes again stand out (Fig. 6).
 |
In the following subsections we will look at the growth sequences for
each morphology in more detail. We also examine the unusual structures
that occur for the larger clusters at low ![]() , which, as we will see,
involve a mixture of order and disorder.
, which, as we will see,
involve a mixture of order and disorder.