Icosahedral clusters

Many small clusters are polytetrahedral in the sense that the whole of the cluster can be divided into tetrahedra. This category includes the 13-atom icosahedron, which can be decomposed into twenty tetrahedra sharing a common vertex. Addition of atoms to the icosahedron can occur in two ways and the two types of overlayer that result are illustrated in Fig. 7. One growth mode (fcc-like) continues the fcc packing of the twenty strained tetrahedra making up the icosahedron, and leads to the 55-atom Mackay icosahedron (Fig. 1(b)). This scheme introduces octahedral interstices, and so the resulting structures are no longer polytetrahedral. The other `anti-Mackay' (hcp-like) growth mode involves sites which are hcp with respect to the tetrahedra. For growth on the 13-atom icosahedron, this overlayer preserves polytetrahedral character. Each of the vertices of the original icosahedron becomes icosahedrally coordinated, and the structure that results from the completion of this overlayer, 45A, is a rhombic tricontahedron; it is an icosahedron of interpenetrating icosahedra. Interestingly, the rhombic tricontahedron is the face-dual of the truncated icosahedron made famous by $\rm C_{60}$; indeed, it is even a particularly stable shell for the coverage of a $\rm C_{60}$ molecule by alkaline earth metal atoms.[73] In previous studies, the anti-Mackay overlayer has been referred to as the polyicosahedral[1] or the face-capping overlayer.[6] Such names are reasonable for growth on the 13-atom icosahedron, but are confusing for growth on larger Mackay icosahedra.

  

Figure 7: Atomic positions for the two possible overlayers of the icosahedron, anti-Mackay (left) and Mackay (right). These are shown for a single face of the icosahedron.

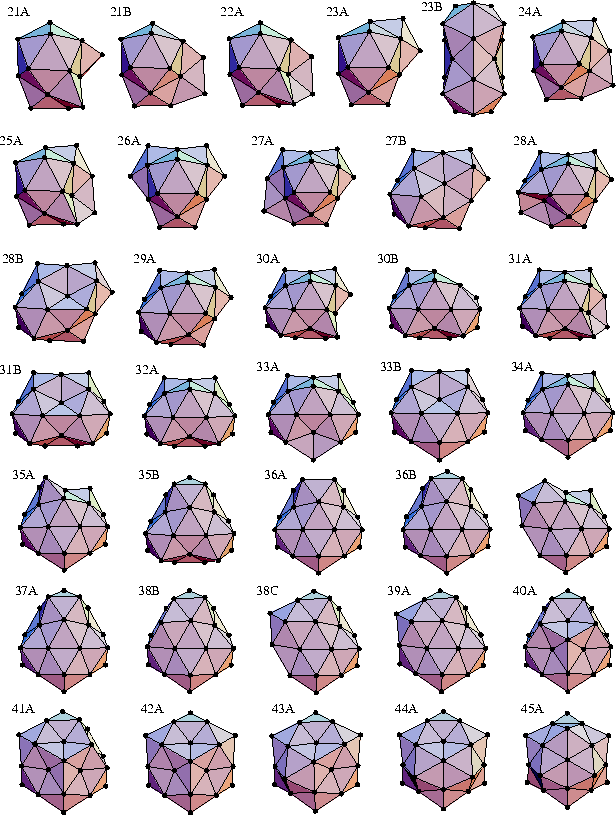
The icosahedral structures with an anti-Mackay overlayer are illustrated in Fig. 8 and those with a Mackay overlayer in Fig. 9. Growth from the 13-atom icosahedron begins in the anti-Mackay positions, because these do not include any low-coordinate edge sites, thus giving a larger n_nn. However, at some critical size the Mackay overlayer becomes lower in energy because of the larger strain energies associated with the anti-Mackay overlayer. Further growth then leads to the next Mackay icosahedron. The size at which this change occurs depends on the range of the potential; it is given by the dashed line of negative slope that divides the icosahedral region of the phase diagram (Fig. 4). The crossover size increases with the range of the potential.

  

Figure 8: Icosahedral global minima formed by growth of an anti-Mackay overlayer on the 13-atom icosahedron, except structure 23B which is composed of two face-sharing icosahedra.

At $\rho_0=6$ the Mackay overlayer is the lowest in energy for $N\ge32$; the corresponding result for LJ clusters is $N\ge31$.In ab initio molecular dynamics calculations for lithium clusters,[74] the anti-Mackay overlayer is lowest in energy up to N=45. Similarly, polytetrahedral structures were observed in a tight-binding study of sodium clusters up to the largest size considered N=34 (for which 34A was the most stable structure).[75] These effects are nicely explained by the long range of alkali metal potentials.

Especially stable structures with an anti-Mackay overlayer occur when the icosahedral coordination of a vertex atom is complete. These structures give rise to the peaks in $\Delta_2 E$ at N=19, 23 26, 29, 34 and 45 for $\rho_0$=3; only the first four of these peaks are seen at $\rho_0$=6, and only the first at $\rho_0$=10 (Fig. 5). Some of these magic numbers have been observed in the mass spectra of noble gases[22,23,24] and even barium.[76] The centres of the icosahedra in these structures form a dimer for 19A, an equilateral triangle for 23A, a tetrahedron for 26A, a trigonal bipyramid for 29A, a pentagonal bipyramid for 34A, and an icosahedron for 45A.

At a number of sizes there is more than one global minimum with an anti-Mackay overlayer for different values of $\rho_0$.The transitions between these structures are related to small differences in the value of $E_{\rm strain}$. Also illustrated in Fig. 8 is structure 23B, which is made up of two face-sharing icosahedra. It can be formed from structure 17B by the addition of six atoms to part of the overlayer.

  

Figure 9: Icosahedral global minima formed by growth of a Mackay overlayer on the 13-atom icosahedron.

The first global minimum with a Mackay overlayer occurs at N=27. Especially stable structures occur at those sizes for which complete faces of the 55-atom Mackay icosahedra are missing. These structures give rise to the peaks at N=39, 46 and 49 for $\rho_0$=6 and correspond to 5, 2 and 1 missing faces, respectively. Again, these magic numbers have been seen in the mass spectra of noble gases.[23]

Structure 38E has an atom missing from a vertex of the original 13-atom icosahedron to allow the overlayer to complete a particularly stable form. This structure was not found in Northby's study, but it is the lowest energy LJ icosahedral cluster.[62]

  

Figure 10: Icosahedral global minima formed by growth from the 55-atom Mackay icosahedron.

The icosahedral global minima with more than 55 atoms are shown in Fig. 10. As for the 13-atom icosahedron, growth initially occurs at the anti-Mackay sites, because this results in structures with larger n_nn. Completion of this overlayer occurs for a cluster with 127 atoms. The vertices of the 55-atom Mackay icosahedron become icosahedrally coordinated, but the edge atoms have a decahedral coordination shell (this is clearly visible for 59D) leading to the half octahedra that are visible in the surface layers of the anti-Mackay clusters. The most prominent peak in $\Delta_2 E$ due to an anti-Mackay structure occurs at N=71 for $\rho_0$=6. This corresponds to an overlayer which completely covers the five faces surrounding a vertex of the underlying icosahedron. There are smaller peaks at N=58, 61, and 64, which correspond to complete coverage of one, two and three faces, respectively.

Structure 69C has a vertex atom missing from the underlying Mackay icosahedron like 38A. There are also structures (62C, 65D, 72C and 75B) where an atom is added to the surface of the overlayer rather than to the Mackay icosahedron. Again there are transitions between different anti-Mackay structures resulting from small differences in $E_{\rm strain}$.

The first structure in this size range with a Mackay overlayer is 78D. We expect that the crossover from an anti-Mackay to a Mackay overlayer will again shift to larger size as the range increases, but we have not investigated this prediction in the present work. There are also three icosahedral global minima, 69B, 70C and 71B, which do not fit neatly into either the Mackay or anti-Mackay category. Their surface layers have a Mackay-like character, but are not in correct alignment with the underlying icosahedron. The overlayer has been given a twist about one of the fivefold axis in order to collapse some of the half octahedra at the edge of the overlayer into trigonal bipyramids in a multiple diamond-square-diamond (DSD) process.[77] In fact for $\rm M_{71}$ at $\rho_0$=5, the lowest energy Mackay structure is a C_5v transition state corresponding to a multiple DSD rearrangement between two permutational isomers of 71B.

Fig. 6 illustrates the variation of the icosahedral energies with size. The complete Mackay icosahedra appear as narrow minima separated by broad maxima corresponding to structures with incomplete outer shells. At $\rho_0$=6 it is only near the top of these maxima that fcc and decahedral structures begin to have similar energies, for example at N=38 and 75.