The samples of M13 stationary points were produced by the method
described in the previous section.
For ![]() =3, 4, 6, 10 and 14 we used as our values of nev 15, 15, 6, 3 and 2, respectively.
The decreasing number of eigenvectors searched at shorter range was necessary because of the
escalating requirements for computer time and disk space to generate and store the data
for such large samples of stationary points.
Consequently, the incompleteness of the samples is likely to increase with
=3, 4, 6, 10 and 14 we used as our values of nev 15, 15, 6, 3 and 2, respectively.
The decreasing number of eigenvectors searched at shorter range was necessary because of the
escalating requirements for computer time and disk space to generate and store the data
for such large samples of stationary points.
Consequently, the incompleteness of the samples is likely to increase with ![]() and be greater for the transition states than minima.
The size of the samples is given in Table 2.1 and some of the
average properties are catalogued in Table 6.1.
Some properties have a fairly simple dependence on
and be greater for the transition states than minima.
The size of the samples is given in Table 2.1 and some of the
average properties are catalogued in Table 6.1.
Some properties have a fairly simple dependence on ![]() .For example, the increase in the mean vibrational frequency as the range decreases
correlates with the increased curvature of the pair potential at its minimum (Figure 2.2).
.For example, the increase in the mean vibrational frequency as the range decreases
correlates with the increased curvature of the pair potential at its minimum (Figure 2.2).
| 0.216 | 0.340 | 0.682 | 1.843 | 3.680 | |
| nts | 4.89 | 8.26 | 11.54 | 8.04 | 8.52 |
| ngm | 1.00 | 1.38 | 2.40 | 3.65 | 3.70 |
| Sgm / r0 | 2.597 | 3.079 | 3.884 | 3.952 | 3.770 |
| 0.184 | 0.262 | 0.469 | 1.051 | 1.450 | |
| S/r0 | 3.012 | 2.905 | 1.874 | 1.119 | 1.083 |
| D/r0 | 1.607 | 1.477 | 1.169 | 0.842 | 0.819 |
| 0.114 | 0.483 | 0.545 | 0.585 | 0.786 | |
| 4.512 | 3.693 | 2.087 | 1.473 | 1.540 | |
| 4.398 | 3.210 | 1.542 | 0.888 | 0.786 | |
| 7.161 | 5.269 | 4.748 | 5.051 | 4.889 | |
| nbasin | 1 | 1 | 3 | 54 | 262 |
More interesting are those properties that give insight into the global topography of the PES.
As can be seen from Figure 4.4 the energy gap
between the global minimum, the 13-atom icosahedron, and the other low-lying minima
decreases as ![]() is increased.
This flattening of the surface is also apparent in the average values of
is increased.
This flattening of the surface is also apparent in the average values of ![]() ,
the difference in energy between two connected minima;
,
the difference in energy between two connected minima; ![]() is effectively
a local measure of the slope of the PES.
is effectively
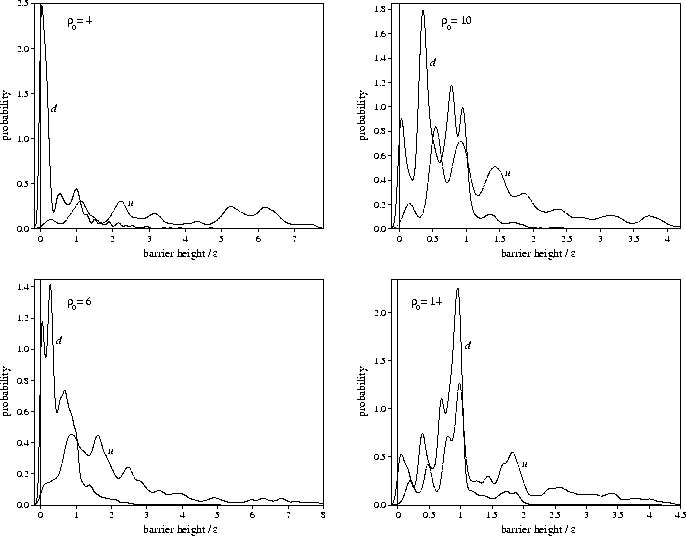
a local measure of the slope of the PES.![[*]](foot_motif.gif) The averages of the barrier heights show that the barrier to go downhill (bd) increases with
The averages of the barrier heights show that the barrier to go downhill (bd) increases with ![]() .At
.At ![]() =4, the probability distribution of bd is dominated by the
low barrier peak (Figure 6.1), but
as
=4, the probability distribution of bd is dominated by the
low barrier peak (Figure 6.1), but
as ![]() increases the magnitude of this peak diminishes.
The greater similarity between the distributions for bd and bu at larger
increases the magnitude of this peak diminishes.
The greater similarity between the distributions for bd and bu at larger ![]() is
a reflection of the smaller value of
is
a reflection of the smaller value of ![]() .
We expect, based on the results of Chapter 5, that the combined effect
of the larger downhill barriers and the flatter PES will be to make relaxation to the
global minimum more difficult at shorter range.
.
We expect, based on the results of Chapter 5, that the combined effect
of the larger downhill barriers and the flatter PES will be to make relaxation to the
global minimum more difficult at shorter range.
 |
In a comparison of the topographies of Lennard-Jones and potassium chloride clusters,
it was noted that the rearrangements for potassium chloride clusters were much more cooperative[252].
It was suggested that this might have been one of the reasons for the greater ease with
which the potassium chloride clusters could reach the global minimum.
The moment ratio of displacement, ![]() , can be used to measure the
cooperativity of a rearrangement. It is defined by[286]
, can be used to measure the
cooperativity of a rearrangement. It is defined by[286]
![\begin{displaymath}
\gamma = { N \sum_i \left[Q_i(s)-Q_i(t)\right]^4 \over
\left( \sum_i \left[Q_i(s)-Q_i(t)\right]^2 \right)^2 }, \end{displaymath}](img351.gif) |
(6.1) |
 |
The shortest reaction pathway to the global minimum was calculated for each minimum on the PES.
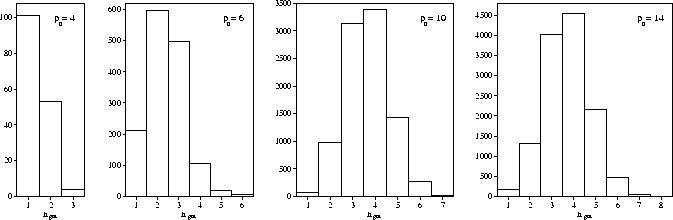
If we look at ngm, the number of steps between minima along one of these pathways,
it is clear that ngm increases as the range decreases (Figure 6.2).
At ![]() =3 all the minima are directly connected to the global minimum, yet at
=3 all the minima are directly connected to the global minimum, yet at ![]() =14,
a minimum can be as far as eight steps away.
The ngm histograms also show that the connectivity patterns for the M13 PES
are quite different from the standard model PES that we considered in Chapter 5
for which the number of minima increased exponentially with the number
of steps away from the global minimum.
It is also interesting to note the large number of minima that are directly
connected to the global minimum.
For example, at
=14,
a minimum can be as far as eight steps away.
The ngm histograms also show that the connectivity patterns for the M13 PES
are quite different from the standard model PES that we considered in Chapter 5
for which the number of minima increased exponentially with the number
of steps away from the global minimum.
It is also interesting to note the large number of minima that are directly
connected to the global minimum.
For example, at ![]() =6 we found 568 geometrically distinct transition states which connect
the icosahedron to 213 geometrically distinct minima.
If one takes into account the reaction path degeneracy, the number of transition states
surrounding a single permutational isomer of the icosahedron is at least
=6 we found 568 geometrically distinct transition states which connect
the icosahedron to 213 geometrically distinct minima.
If one takes into account the reaction path degeneracy, the number of transition states
surrounding a single permutational isomer of the icosahedron is at least ![]() .
.
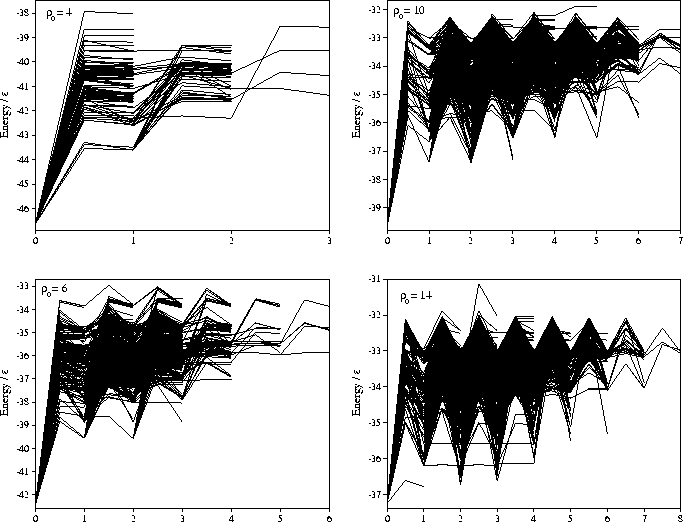 |
In Figure 6.3, we show the shortest reaction path to
the global minimum for each minimum.
Again the larger barrier heights and the increased flatness of the PES
are apparent at short range.
At ![]() =14 there are clearly some pathways for which the minima
do not monotonically decrease in energy as the global minimum is approached.
This will be considered further when we examine the basin structure of the PES.
=14 there are clearly some pathways for which the minima
do not monotonically decrease in energy as the global minimum is approached.
This will be considered further when we examine the basin structure of the PES.
 |
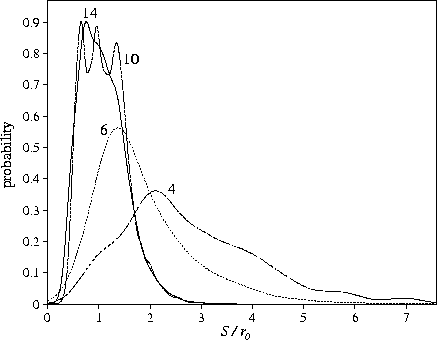
Although ngm increases with ![]() the average total length of the reaction paths in
configuration space (Sgm) is relatively constant for
the average total length of the reaction paths in
configuration space (Sgm) is relatively constant for ![]() , and for smaller
, and for smaller
![]() shows a much weaker dependence on the range than ngm (Table 6.1 and Figure 6.4).
This is not too surprising if we consider the dependence of the path length for
a single rearrangement on
shows a much weaker dependence on the range than ngm (Table 6.1 and Figure 6.4).
This is not too surprising if we consider the dependence of the path length for
a single rearrangement on ![]() : this length decreases significantly as the range is reduced (Figure 6.5).
The pathways simply become more rugged rather than longer: more transition states must be crossed.
: this length decreases significantly as the range is reduced (Figure 6.5).
The pathways simply become more rugged rather than longer: more transition states must be crossed.
 |
The topology of the surface was further analysed in terms of the
structure of the basins on the PES.
For ![]() =3 and 4, every minimum lies on a sequence of minima which are monotonically
decreasing in energy and lead down to the global minimum; the PES consists of a single basin.
For
=3 and 4, every minimum lies on a sequence of minima which are monotonically
decreasing in energy and lead down to the global minimum; the PES consists of a single basin.
For ![]() =6 all but two of the minima lie on such monotonic sequences.
By Kunz and Berry's definition these two minima also represent basin bottoms, albeit
very shallow; only one step needs to be taken to reach a
minimum in the basin surrounding the icosahedron.
For
=6 all but two of the minima lie on such monotonic sequences.
By Kunz and Berry's definition these two minima also represent basin bottoms, albeit
very shallow; only one step needs to be taken to reach a
minimum in the basin surrounding the icosahedron.
For ![]() =10 and 14 many more shallow basins appear on the PES (Table 6.1).
Despite this increase in the number of basins, 96.8% of the minima located are in the icosahedral basin
for
=10 and 14 many more shallow basins appear on the PES (Table 6.1).
Despite this increase in the number of basins, 96.8% of the minima located are in the icosahedral basin
for ![]() =14 (Figure 6.6e).
=14 (Figure 6.6e).
One consequence of the definition of a basin is that it is possible for a minimum to lie on monotonic sequences which lead down to the bottom of different basins. Indeed high energy minima may lie in numerous basins (Figure 6.6f). In this regard the division of minima space into basins differs from the division of configuration space into wells surrounding minima, since there is no equivalent of the steepest descent path which uniquely maps each point in configuration space to a minimum. Instead the division of minima space is more like a Venn diagram where overlap can occur between regions.
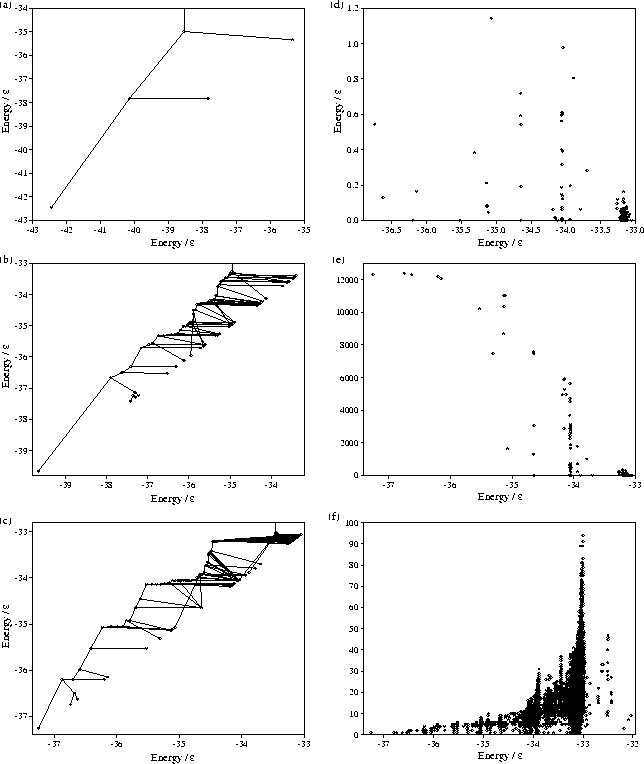 |
One method to analyse this basin structure is with `tree' diagrams (Figure 6.6); these are in some ways similar to the equilibration trees considered in Chapter 5. Two basins are considered to become `connected' and to form a new metabasin when the energy is that of the lowest energy minimum which lies in both basins. Each point in the tree diagram represents a basin or the creation of a new metabasin, and the nodes occurs at the energies at which the basins or metabasins become connected. The tree diagrams, therefore, follow the pattern of connections that occurs between basins and metabasins as the energy is increased.
It is noticeable that in the tree diagrams virtually all the basins are directly
connected to the line corresponding to the metabasin of the global minimum,
i.e. the basin which requires least energy to enter is the metabasin of the global minimum.
The basin surrounding the global minimum is clearly the dominant feature even on the more
rugged PES's for ![]() =10 and 14.
Furthermore, many of the lines joining a basin to the icosahedral basin are virtually horizontal
implying that the depth of most basins (measured in terms of the energy, relative to the basin bottom,
of the lowest energy minimum that is also in another basin) is small (Figure 6.6d).
The average depths for
=10 and 14.
Furthermore, many of the lines joining a basin to the icosahedral basin are virtually horizontal
implying that the depth of most basins (measured in terms of the energy, relative to the basin bottom,
of the lowest energy minimum that is also in another basin) is small (Figure 6.6d).
The average depths for ![]() =10 and 14 are 0.237 and
=10 and 14 are 0.237 and ![]() , respectively.
Most of the basins are not sufficiently deep to act as effective traps.
The lower average depth for
, respectively.
Most of the basins are not sufficiently deep to act as effective traps.
The lower average depth for ![]() =14 results from the large number of very shallow basins at high energy;
163 of the 262 basins lie above
=14 results from the large number of very shallow basins at high energy;
163 of the 262 basins lie above ![]() .
.
Although the PES's at ![]() =10 and 14 involve a large number of basins, these PES's do not equate
with the multiple funnel scenarios outlined in §5.4 since the basins are too shallow for them
to be categorized as separate funnels.
However, their roughness is still likely to hinder relaxation to the global minimum,
even if not to as large an extent as multiple funnels.
=10 and 14 involve a large number of basins, these PES's do not equate
with the multiple funnel scenarios outlined in §5.4 since the basins are too shallow for them
to be categorized as separate funnels.
However, their roughness is still likely to hinder relaxation to the global minimum,
even if not to as large an extent as multiple funnels.