Searching the potential energy surface

 The main method that we have used to generate candidate structures for the global minima makes use of the physical insight gained from the last section. We have simply attempted to construct those structures that maximize n_nn for the three ordered morphologies. The resulting geometries were then minimized by either the conjugate gradient[87] or eigenvector-following[88] methods. A similar approach was successfully used by Northby to generate low energy icosahedral structures for LJ clusters[50]. The effectiveness of this method is reflected by how few of Northby's lowest energy structures have been superseded and by the length of time that it has taken to find these exceptions[69,70,71,72,73]. As we will show in §2.4, some of the global minima that we have found by this method may be extremely difficult to find by an `ab initio' global optimization method. This method, though, does depend on the imagination of the practitioner to conceive of all the possible ways that a structure with a large value of n_nn could be obtained. Furthermore, the method will always fail to find the global minima if the latter is not based on one of the ordered types of cluster structure, as is the case for the larger clusters we have considered at low values of $\rho_0$.

Therefore, complementary to the above method, a number of global optimization techniques were used to try to find structures that might have been missed. First, we used molecular dynamics to explore the PES and generate configurations for minimization. Using high energy runs large regions of the PES are sampled, whereas low energy runs allow a more detailed search of a local region of the PES. Secondly, we used a method in which eigenvector-following is employed to take steps directly between minima on the PES[89]. If low temperature Metropolis Monte Carlo is used in this space of minima, the system will walk down to the bottom of a basin containing many minima. This technique avoids the difficulties associated with trapping in local minima that can occur for methods which take steps directly in configuration space. It is outlined further in Chapter 6. Thirdly, we used a global optimization method developed by David Wales which employs a `basin hopping' technique.

 

$$\rho_0=3 \rho_0=4 \rho_0=6 \rho_0=10 \rho_0=14$$

minima 9 159 1441 9290 12717

transition states 27 687 8380 37499 54444

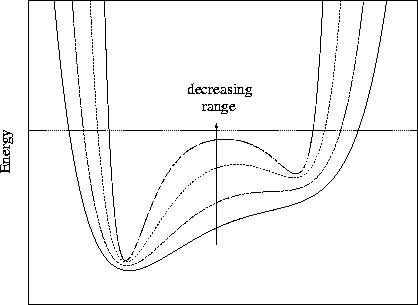
The above three global optimization methods are least successful for short-ranged potentials. This is because the PES become more rugged as the range is decreased. As illustrated in Table 2.1 for 13, the number of minima and transition states on the PES increases with $\rho_0$. The physical reason for the larger number of minima at short range is the loss of accessible configuration space as the potential wells become narrower, thus producing barriers where there are none at long range. This effect is shown schematically in Figure 2.4.

  

Figure 2.4: Schematic diagram to show how a higher energy minimum can be `swallowed up' by a lower energy minimum as the range of the potential increases.

Barrier heights are also likely to become higher and rearrangements more localized for a shorter-ranged potential. These trends have been observed in comparisons of the rearrangements of 55-particle C₆₀ and LJ clusters[90]. Other effects are noted in a detailed analysis of the topography of the 13 PES in §6.3. These changes imply that the range of the potential is likely to have a significant effect on the dynamics, making escape from local minima much more difficult. This has been illustrated by Rose and Berry who have shown that the rate at which the ground state structure of a potassium chloride cluster is found upon cooling can be significantly decreased by using a shielded Coulomb potential to reduce the range of the interactions[91]. Similarly, Stillinger and Stillinger[92] and Bytheway and Kepert[60] both found that minimizations performed from random starting configurations are much more likely to find the global minimum for a long-ranged potential.

Finding the global minimum at short range can also be harder for a more subtle reason. Fcc and decahedral minima have a smaller degree of structural similarity with the large number of minima typical of the liquid-like state than the icosahedral structures. Therefore, the paths from the liquid-like state to the decahedral structures are likely to be fewer and longer than those to the icosahedral structures. This effect will be considered in more depth later in the thesis.

It must be emphasized, though, that none of these methods are guaranteed to find the global minimum. Finding the global minima for a PES with so many degrees of freedom is an NP-hard problem[93]. Morse clusters, however, provide an ideal system to compare different global optimization methods both because the complexity of the PES can be systematically varied by changing a single parameter and because this study provides a comprehensive catalogue of likely global minima.