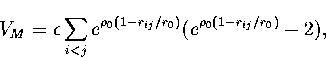
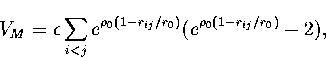 |
(2.1) |
The structure of a cluster is given by the structure(s) associated with the global free energy minimum. At zero temperature, the structure with the lowest free energy is simply the global minimum of the PES. At higher temperatures, entropic factors must also be considered. Although we only perform a comprehensive survey of the zero Kelvin structure, some examples of the structural effects of temperature are discussed in §2.4.
To understand what factors cause a structure to have low potential energy and how these
change with the value of the range parameter, ![]() , it is instructive to look more closely
at the form of the potential.
The energy can be partitioned into three contributions as follows,
, it is instructive to look more closely
at the form of the potential.
The energy can be partitioned into three contributions as follows,
| |
(2.2) |
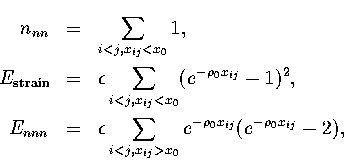
(2.3)
The dominant term in the energy comes from nnn. Ennn is a smaller term and its value varies in a similar manner to nnn. It is only likely to be important in determining the lowest energy structures when other factors are equal. For example, bulk fcc and hexagonal close-packed (hcp) lattices both have twelve nearest neighbours per atom. Next-nearest neighbour interactions are the cause of the lower energy of the hcp crystal when a pair potential such as the LJ form is used[83,84]. Non-nearest neighbour interactions also cause the contraction of nearest neighbour distances from the equilibrium pair value and this contraction increases with the range of the potential[41].
![]() , which measures the energetic penalty for the deviation of a nearest-neighbour distance
from the equilibrium pair distance, is a key quantity in this analysis.
It should not be confused with strain due to an applied external force.
For a given geometry,
, which measures the energetic penalty for the deviation of a nearest-neighbour distance
from the equilibrium pair distance, is a key quantity in this analysis.
It should not be confused with strain due to an applied external force.
For a given geometry, ![]() grows rapidly with increasing
grows rapidly with increasing ![]() because the potential well narrows.
This can be seen by taking a Taylor expansion of
because the potential well narrows.
This can be seen by taking a Taylor expansion of ![]() about xij=0:
about xij=0:
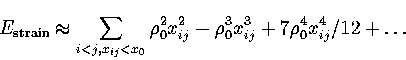 |
(2.4) |
From this analysis we can see that minimization of the potential energy involves a balance
between maximizing nnn, and minimizing ![]() .
The interior atoms of the three morphologies (Figure 2.1) all have twelve nearest neighbours, and
so differences in nnn arise from surface effects.
The optimal shape for each morphology results from the balance between maximizing the
proportion of
.
The interior atoms of the three morphologies (Figure 2.1) all have twelve nearest neighbours, and
so differences in nnn arise from surface effects.
The optimal shape for each morphology results from the balance between maximizing the
proportion of ![]() faces (an atom on a
faces (an atom on a ![]() face is 9-coordinate,
but on a
face is 9-coordinate,
but on a ![]() face only 8-coordinate) and minimizing the fraction of atoms in the surface layer.
As Mackay icosahedra (Figure 2.1b) have only
face only 8-coordinate) and minimizing the fraction of atoms in the surface layer.
As Mackay icosahedra (Figure 2.1b) have only ![]() faces and are approximately spherical,
the icosahedral structures have the largest nnn.
Complete Mackay icosahedra occur at
faces and are approximately spherical,
the icosahedral structures have the largest nnn.
Complete Mackay icosahedra occur at ![]() A pentagonal bipyramid has all
A pentagonal bipyramid has all ![]() faces, but as it is not very spherical
more stable decahedral forms are obtained by truncating the structure parallel
to the five-fold axis to reveal five
faces, but as it is not very spherical
more stable decahedral forms are obtained by truncating the structure parallel
to the five-fold axis to reveal five ![]() faces and then
introducing re-entrant
faces and then
introducing re-entrant ![]() faces between adjacent
faces between adjacent ![]() faces.
The resulting structure is called a Marks' decahedron (Figure 2.1c) and
was first predicted by the use of a modified Wulff construction[85].
The decahedral structures have lower values of nnn than icosahedral structures
because of the presence of the
faces.
The resulting structure is called a Marks' decahedron (Figure 2.1c) and
was first predicted by the use of a modified Wulff construction[85].
The decahedral structures have lower values of nnn than icosahedral structures
because of the presence of the ![]() faces.
The tetrahedron and octahedron are fcc structures that have only
faces.
The tetrahedron and octahedron are fcc structures that have only ![]() faces but
they are not very spherical.
The optimal fcc structure is the truncated octahedron with regular hexagonal faces
(Figure 2.1a).
At larger sizes than those considered in this study, the optimal structure involves further facetting,
so that it more closely approximates the Wulff polyhedron[86].
Of the three morphologies fcc structures have the lowest values of nnn.
faces but
they are not very spherical.
The optimal fcc structure is the truncated octahedron with regular hexagonal faces
(Figure 2.1a).
At larger sizes than those considered in this study, the optimal structure involves further facetting,
so that it more closely approximates the Wulff polyhedron[86].
Of the three morphologies fcc structures have the lowest values of nnn.
 |
Having deduced the relative values of nnn and ![]() for icosahedral, decahedral
and fcc structures, we can predict the effect of the range on the competition between the three
morphologies.
For a moderately long-ranged potential, the strain associated with the icosahedral structures
can be accommodated without too large an energetic penalty and so they are the most stable.
As the range of the potential is decreased, the strain energy associated with the icosahedral
structures increases rapidly, and there comes a point where decahedral structures become more stable.
Similarly, for a sufficiently short-ranged potential fcc structures become more stable than
decahedral structures.
for icosahedral, decahedral
and fcc structures, we can predict the effect of the range on the competition between the three
morphologies.
For a moderately long-ranged potential, the strain associated with the icosahedral structures
can be accommodated without too large an energetic penalty and so they are the most stable.
As the range of the potential is decreased, the strain energy associated with the icosahedral
structures increases rapidly, and there comes a point where decahedral structures become more stable.
Similarly, for a sufficiently short-ranged potential fcc structures become more stable than
decahedral structures.
The decomposition of the potential energy also helps us to understand the effect of size on the
energetic competition between the three morphologies.
The differences in nnn between the morphologies, which arise from their different
surface structures, are approximately proportional to the surface area (![]() ).
The strain energies, though, are proportional to the volume (
).
The strain energies, though, are proportional to the volume (![]() ).
Therefore, the differences in
).
Therefore, the differences in ![]() increase more rapidly with
size than the differences in nnn, thus explaining the changes in the most stable
morphology from icosahedral to decahedral to fcc with increasing size.
The effect of increasing the size is similar to the effect of decreasing
the range of the potential: both destabilize strained structures.
The most favourable morphology varies with both the size of the cluster and the range of the potential.
increase more rapidly with
size than the differences in nnn, thus explaining the changes in the most stable
morphology from icosahedral to decahedral to fcc with increasing size.
The effect of increasing the size is similar to the effect of decreasing
the range of the potential: both destabilize strained structures.
The most favourable morphology varies with both the size of the cluster and the range of the potential.