Introduction

Structure has a central role in cluster science and is a prerequisite for elucidating many of the properties of clusters. As a consequence, much experimental and theoretical effort has been expended in order to characterize cluster structure. Indeed, many of the experimental methods for obtaining structural information take advantage of the sensitive dependence of cluster properties, such as chemical reactivity[39] and magnetism[40], on cluster structure.

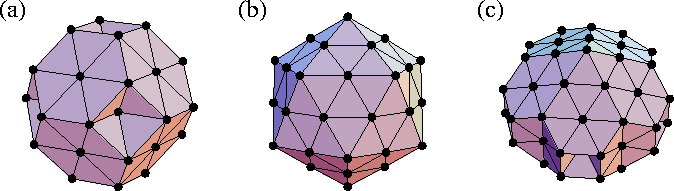
One of the most interesting aspects of cluster structure is the possibility of non-crystallographic symmetry which arises from the absence of translational periodicity. In particular, many clusters are found to have fivefold axes of symmetry. The three main types of ordered structure that simple atomic clusters adopt are close-packed, decahedral and icosahedral. Examples of each are given in Figure 2.1. The decahedral structures have a single fivefold axis of symmetry and are based on pentagonal bipyramids, and the icosahedral structures have six fivefold axes of symmetry.

  

Figure 2.1: Three examples of the structures clusters can adopt: (a) a 38-atom truncated octahedron, (b) a 55-atom Mackay icosahedron, and (c) a 75-atom Marks' decahedron. These clusters have the optimal shape for the three main types of ordered packing seen in clusters: face-centred cubic (fcc), icosahedral and decahedral, respectively. The latter two structural types cannot be extended to bulk because of the presence of five-fold axes of symmetry.

Icosahedral structures were first discovered in investigations of clusters bound by the Lennard-Jones (LJ) potential[41]. Although early theoretical studies considered structures that were fragments of a crystalline lattice, it soon became clear that the lowest energy structures were based on Mackay icosahedra[42]. The LJ potential provides a reasonable description of the interaction between rare gas atoms, and it has been confirmed by electron diffraction[43,44,45,46] and mass spectroscopy[47,48,49] that rare gas clusters are icosahedral for sizes up to at least 750 atoms. Furthermore, the detailed intensity variations in the mass spectra show very good agreement with those expected from the icosahedral growth sequence of LJ clusters[50]. Icosahedral structures have since been found for many other gas phase clusters, including metals[51,52,53,54,55,56], and molecular clusters[57,58]. Icosahedral and decahedral structures are also commonly observed for metal clusters supported on surfaces[1]. At sufficiently large sizes, though, there must be a crossover to the bulk limit where crystalline structures have the lowest energy.

The focus of this chapter is to elucidate the relationship between the form of the interatomic potential and the structure of clusters. Many studies have concentrated on the structures of clusters exhibited by a specific functional form, including model potentials such as the LJ potential and those designed for a particular material. Fewer studies have examined the general structural effects of the different contributions to the potential. For this purpose, it is useful to consider a potential which is simple enough that the effects of any changes made to its form can be understood and that these changes can be made by varying a single parameter. This method has been used to investigate the effect of the range[59,60,61] and anisotropy[62,63] of the potential on the structure and phase behaviour of small clusters.

In this chapter we further investigate the effects of the range of the potential. Previous studies have found that as the range is increased the number of minima and saddle points on the PES decreases; the PES becomes smoother and simpler[59,64,65]. Furthermore, Bytheway and Kepert noted that, for a sufficiently long-ranged potential, structures based on icosahedral packings become less favoured energetically than structures with even higher coordination[60]. Little, however, has been discovered about the structures associated with shorter-ranged potentials, and the effects of the range and size on the competition among icosahedral, decahedral and close-packed structures. Here we address these issues by examining clusters of atoms bound by the Morse potential. We consider all clusters containing up to 80 atoms, and in particular we attempt to find the global minimum as a function of the range and size.

Such a study provides the most comprehensive model of cluster structure in the literature, having a wider range of applicability and exhibiting a much greater diversity of structural behaviour than observed for LJ clusters, the most well-studied cluster system. The structural catalogue provided by this study will be useful for experimentalists, as they can only obtain indirect structural information which, in order to be assigned, must be compared to that expected for model structures. This is particularly so for chemical probe studies which can obtain detailed information about individual sizes[66,67,68]. This structural database also provides a useful test of global optimization methods, and would represent a much tougher and more general examination than that provided by LJ clusters which are commonly used as a test system.

The known behaviour of LJ clusters provides a useful starting point for our study. For the majority of small sizes, icosahedral clusters are the lowest in energy. Northby has conducted a systematic survey for $13\le N\le 147$to find the lowest energy minima based on icosahedral structures[50]. Some of his results have since been superseded[69,70,71,72,73]. Of particular interest are the few sizes at which the lowest energy structures are not icosahedral, but instead decahedral or fcc[70,71,72]. For larger systems sequences of clusters with the optimal shape for the different morphologies have been compared[74,75,76]. In these comparisons, the energy is interpolated between the values of N for each cluster of the sequence. The values of N at which the lowest energy lines cross are indicators of the size for which a structural transition is likely to occur. These studies have shown that a decahedral sequence becomes most stable at $N\approx 1600$ and an fcc sequence[76] at $N\approx 10^5$.