


Next: Thermodynamics of Small Lennard-Jones
Up: The Structure of Clusters
Previous: Structures at long range
Home: Return to my homepage
In this chapter we have attempted to find the global minimum for Morse clusters as a function of
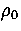 and the number of atoms.
The global minimum represents the equilibrium structure at zero Kelvin.
However, we need to consider how important the global minimum is
in determining the structure at finite temperature.
To answer this question we have to examine the effects of other local minima on the PES.
The thermodynamic properties of a collection of minima can be approximated
by superposition of the density of states from each minimum,
as described in detail in Chapter 3.
and the number of atoms.
The global minimum represents the equilibrium structure at zero Kelvin.
However, we need to consider how important the global minimum is
in determining the structure at finite temperature.
To answer this question we have to examine the effects of other local minima on the PES.
The thermodynamic properties of a collection of minima can be approximated
by superposition of the density of states from each minimum,
as described in detail in Chapter 3.
Table 2.3:
The ten lowest energy decahedral and icosahedral minima found for 75 at 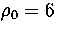 .
.
| |
decahedral |
|
|
|
icosahedral |
|
Energy/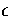 |
nnn |
|
Energy/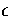 |
nnn |
|
-351.472365 |
D5h |
319 |
|
-351.177041 |
C1 |
328 |
| -349.500086 |
C1 |
317 |
|
-351.139799 |
C1 |
328 |
| -349.498552 |
C1 |
317 |
|
-351.135122 |
Cs |
328 |
| -349.498393 |
C1 |
317 |
|
-350.984741 |
C1 |
328 |
| -349.496058 |
C1 |
317 |
|
-350.912649 |
C1 |
328 |
| -349.489864 |
C1 |
317 |
|
-350.890122 |
C1 |
328 |
| -349.275647 |
C1 |
317 |
|
-350.874153 |
C1 |
328 |
| -348.606586 |
C1 |
316 |
|
-350.686821 |
C1 |
327 |
| -348.332763 |
C1 |
316 |
|
-350.612539 |
Cs |
329 |
| -347.636104 |
C1 |
315 |
|
-350.464407 |
C1 |
327 |
Here we apply this method to 75 at 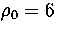 to illustrate the limitations
of finite temperature structural predictions based on knowledge of the global minimum alone.
Sets of low energy decahedral and icosahedral minima were obtained by performing minimizations
from configurations generated by low energy MD runs starting from icosahedral and decahedral
regions of configuration space.
The ten lowest energy minima of each sample are given in Table 2.3.
For 75, the Marks' decahedron, 75C, is the most stable cluster at
to illustrate the limitations
of finite temperature structural predictions based on knowledge of the global minimum alone.
Sets of low energy decahedral and icosahedral minima were obtained by performing minimizations
from configurations generated by low energy MD runs starting from icosahedral and decahedral
regions of configuration space.
The ten lowest energy minima of each sample are given in Table 2.3.
For 75, the Marks' decahedron, 75C, is the most stable cluster at 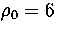 .
There is an energy gap of
.
There is an energy gap of 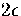 to the next lowest energy decahedral isomer (Table 2.3).
At this value of
to the next lowest energy decahedral isomer (Table 2.3).
At this value of 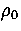 the lowest energy icosahedral structure is only
the lowest energy icosahedral structure is only 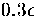 higher
in energy than 75C and there are many icosahedral isomers of similar energy (Table 2.3).
In fact we found 31 icosahedral isomers which were of lower energy
than the second lowest energy decahedral isomer. From this it might be expected
that as the energy is increased the density of states of the icosahedral isomers would become larger
than the decahedral isomers, and so the structure would change from decahedral
to icosahedral with increasing energy or temperature.
higher
in energy than 75C and there are many icosahedral isomers of similar energy (Table 2.3).
In fact we found 31 icosahedral isomers which were of lower energy
than the second lowest energy decahedral isomer. From this it might be expected
that as the energy is increased the density of states of the icosahedral isomers would become larger
than the decahedral isomers, and so the structure would change from decahedral
to icosahedral with increasing energy or temperature.
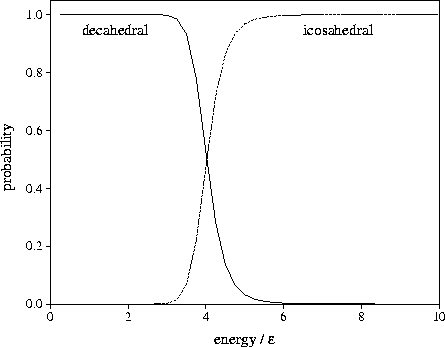
We calculated within the harmonic approximation the equilibrium probabilities
that the structure would be icosahedral or decahedral as a function of the microcanonical total energy.
The results are given in Figure 2.19. From this it can be seen that the equilibrium structure changes from
decahedral to icosahedral when the total energy is only 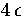 above the bottom of the
lowest well, which corresponds to a reduced temperature of
above the bottom of the
lowest well, which corresponds to a reduced temperature of 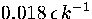 .
It is likely that such a transition would not be observed until higher energies because
of the free energy barrier involved. In fact we once observed this transition in an MD run
started from structure 75C. The run was
.
It is likely that such a transition would not be observed until higher energies because
of the free energy barrier involved. In fact we once observed this transition in an MD run
started from structure 75C. The run was 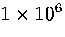 time steps long and at a total energy
of
time steps long and at a total energy
of 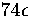 above the lowest well.
above the lowest well.
Figure 2.19:
Calculated equilibrium values for the microcanonical probability that an
75 cluster at 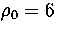 has an icosahedral or a decahedral structure as a function of the total energy.
The energy is measured with respect to the bottom of the well of the Marks' decahedron, 75C.
has an icosahedral or a decahedral structure as a function of the total energy.
The energy is measured with respect to the bottom of the well of the Marks' decahedron, 75C.
 |
This calculation also helps to explain why 75C has not been previously reported
as the lowest energy structure for the much-studied LJ potential.
Global optimization algorithms are often based upon tracking the free energy global minimum
as the temperature is decreased.
This is the principle behind the widely-used simulated annealing method[107].
However, such methods will not find the global minimum if a change in
the free energy global minimum occurs at a temperature where the rate
of isomerization is so low that a transition to the new structure cannot
occur on the time scale of the simulation.
We should not conclude from the above calculation, though, that the global
minimum is not important in understanding cluster structures.
This example is probably an exception rather than the rule.
Such a transition is only likely to occur for values of 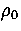 near to where the
global minimum changes and in the above example the cause is clearly the differences
in the energy spectrum of minima for the two morphologies.
In general, then, the global minimum provides a reasonable guide
to the finite temperature structural properties of a cluster,
which can be usefully supplemented by a knowledge
of other low energy minima on the PES.
near to where the
global minimum changes and in the above example the cause is clearly the differences
in the energy spectrum of minima for the two morphologies.
In general, then, the global minimum provides a reasonable guide
to the finite temperature structural properties of a cluster,
which can be usefully supplemented by a knowledge
of other low energy minima on the PES.
If there is a unique low energy global minimum separated by a large energy gap
from higher energy structures it is appropriate to associate the solid-like structure of the cluster with
this single minimum. This would be the case, for example, for the icosahedron 55B at intermediate
ranges of the potential. For the LJ potential, microcanonical simulations
have shown that the 55-atom cluster resides only in the icosahedral potential
well up to an energy of 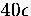 (measured with respect to the bottom of the icosahedral well)
above which the formation of surface defects is observed
and then complete melting[108,109,110,111,112].
However, when there is a set of low energy minima with very similar energies, at all but
very low temperatures an equilibrium ensemble of clusters will contain a mixture of these isomers.
It is therefore more appropriate to associate the `structure' with this set of minima
rather than the global minimum alone.
For example, this would be the case for 55C, which has three other low energy isomers
with the same nnn.
(measured with respect to the bottom of the icosahedral well)
above which the formation of surface defects is observed
and then complete melting[108,109,110,111,112].
However, when there is a set of low energy minima with very similar energies, at all but
very low temperatures an equilibrium ensemble of clusters will contain a mixture of these isomers.
It is therefore more appropriate to associate the `structure' with this set of minima
rather than the global minimum alone.
For example, this would be the case for 55C, which has three other low energy isomers
with the same nnn.
In the above discussion we have been considering the equilibrium structural properties.
However, we also need to consider the question of kinetic versus thermodynamic products.
How important are the low potential energy structures in practice?
When will they actually be found in an experiment?
Van de Waal has suggested that kinetic factors could be essential in the growth
of fcc rare-gas clusters and the nucleation of fcc solid from the LJ liquid[113,114].
Indeed an extremely good fit is obtained to electron diffraction results for argon clusters
from non-optimal structures that involve cross-twinning to allow rapid growth[115,116].
As we noted earlier, the effect of increasing the size and decreasing the range of the potential
is to increase the complexity of the PES.
Therefore, as the range of the potential decreases
the formation of glassy or amorphous clusters, rather than the lowest energy structure,
becomes more likely. Whether this is the case for the larger
clusters we have studied when the potential is short-ranged would require further investigation.
The results for bulk C60 may also provide some insight into this question.
When formed by vapour phase deposition C60 gives an amorphous soot[117],
and only forms the crystalline phase on recrystallization from benzene.
In this chapter we have been considering the effect of the range of attraction
of pair interactions on cluster structure.
As rare gas clusters and clusters of C60 molecules can be reasonably
modelled by pair potentials we would expect the structures we have found at the appropriate 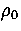 to be very similar to the actual structures of these clusters.
Interestingly, the results lead us to predict that neutral clusters of C60 molecules exhibit
decahedral and fcc structures at small sizes because of the short range of the intermolecular potential.
This basic conclusion has been confirmed in studies using more realistic potentials[95,118].
However, this prediction for neutral cluster differs from experimental results[58] for charged clusters
for which icosahedral structures are observed up to 55 molecules for
to be very similar to the actual structures of these clusters.
Interestingly, the results lead us to predict that neutral clusters of C60 molecules exhibit
decahedral and fcc structures at small sizes because of the short range of the intermolecular potential.
This basic conclusion has been confirmed in studies using more realistic potentials[95,118].
However, this prediction for neutral cluster differs from experimental results[58] for charged clusters
for which icosahedral structures are observed up to 55 molecules for 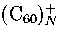 and 147 molecules
for
and 147 molecules
for 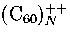 .Given the exceptionally large polarizability of , though,
it is not unreasonable that the introduction of a long range Coulomic term
would significantly affect the energetic competition between morphologies.
Therefore, it would be very interesting if this dramatic difference in structure
between charged and neutral clusters could be observed experimentally, say by electron diffraction.
.Given the exceptionally large polarizability of , though,
it is not unreasonable that the introduction of a long range Coulomic term
would significantly affect the energetic competition between morphologies.
Therefore, it would be very interesting if this dramatic difference in structure
between charged and neutral clusters could be observed experimentally, say by electron diffraction.
In contrast, making predictions for metal clusters from our results is much more
difficult because the range of the potential is only one factor influencing structure.
In particular, many-body terms may also be important[62,63].
These terms may affect the relative surface energies of 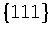 and
and 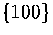 faces,
and so alter the energetic competition between icosahedral, decahedral and fcc structures[102].
For example, in a study of lead clusters cuboctahedra are always found to be lower in energy
than icosahedra because the surface energies of
faces,
and so alter the energetic competition between icosahedral, decahedral and fcc structures[102].
For example, in a study of lead clusters cuboctahedra are always found to be lower in energy
than icosahedra because the surface energies of 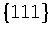 and
and  faces are nearly equal[104].
The value of our results is in providing candidate structures for comparison with the increasingly
detailed structural information being provided by experiments,
such as chemical probe studies[66,67,68],
and for theoretical studies with more realistic,
but also more computationally expensive, descriptions of the interactions.
faces are nearly equal[104].
The value of our results is in providing candidate structures for comparison with the increasingly
detailed structural information being provided by experiments,
such as chemical probe studies[66,67,68],
and for theoretical studies with more realistic,
but also more computationally expensive, descriptions of the interactions.
Our results also allow us to comment on a global optimization method proposed by
Stillinger and Stillinger in which the PES is deformed by increasing the range[92].
We have to echo Chang and Berry's caution[119] that although increasing
the range of a potential does lead to a simplification of the PES
it can also cause large changes in the relative stability of different minima.
The global minimum when a potential is long-ranged may be very different
from the global minimum at the conditions of interest.
For mixtures of spherical colloidal particles and non-adsorbing polymer,
the range of the attractive interaction between the colloidal particles
can be systematically varied by changing the size of the polymer[120].
This effect has been used to study experimentally the phase diagram for such colloidal systems
as a function of the range of the interaction[121,122,123].
We know of no physically realizable system for clusters where the range of the potential could be
similarly varied to cause range-induced transitions in cluster structure.
However, it remains an intriguing possibility.



Next: Thermodynamics of Small Lennard-Jones
Up: The Structure of Clusters
Previous: Structures at long range
Home: Return to my homepage
Jon Doye
8/27/1997
