Structures at long range

**Figure 2.17:** Global minima for small clusters at low values of $\rho_0$ . If appropriate, the disclination network is displayed next to each structure. $-72^\circ$ disclinations are represented by red lines, and $+72^\circ$ disclinations by blue lines.
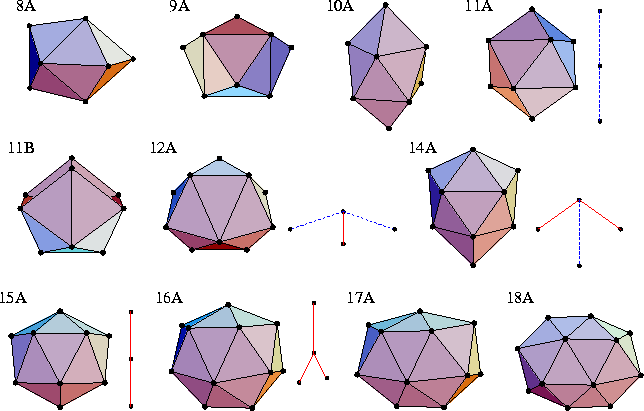
$\begin{figure} \vspace{-0.8cm} \epsfxsize=15cm \centerline{\epsffile{s.low.eps}} \vspace{-1cm}\end{figure}$

The group of structures associated with low $\rho_0$ are close to spherical in shape and in the main are highly strained in order to maximize n_nn. The exceptions are 8A, 9A and 10A (Figure 2.17). These clusters have smaller values of n_nn than the other low energy minima (Figure 2.8), but are more stable because of a larger contribution from E_nnn; the next-nearest neighbour shell is significantly closer than for the incomplete icosahedra. In each case the structures are roughly spherical but do not have an atom in the centre of the cluster.

The majority of the other structures are polytetrahedral, that is the whole volume of the cluster can be divided into tetrahedra with atoms at the vertices. As we noted in §2.3.1, the 13-atom icosahedron is polytetrahedral. In this structure, each nearest-neighbour bond between the centre and a vertex is the common edge of five tetrahedra. This is also true of all the nearest-neighbour bonds of the rhombic tricontahedron (45A) which do not lie on the surface. Nearest-neighbour bonds which are surrounded by a different number of tetrahedra are said to have defects called disclination lines running along the bond. Those bonds with more than five tetrahedra are termed negative disclinations (if there are six it is a $-72^\circ$ disclination, if there are seven a $-144^\circ$ disclination, ...) and those with fewer than five tetrahedra are positive disclinations (if there are four it is a $+72^\circ$ disclination and if there are three a $+144^\circ$ disclination). Most of the structures associated with low $\rho_0$ are polytetrahedral structures that involve disclinations. Although packing five tetrahedra around a nearest-neighbour bond involves some strain, the strain energy associated with packing more or less tetrahedra around a bond is greater. Therefore, structures involving disclinations are only likely to be lowest in energy for long-ranged potentials for which the associated strain can be most easily accommodated, and only if the structures have a larger n_nn than disclination-free structures. A $-72^\circ$ disclination line involves less strain than a $+72^\circ$ disclination line as can be deduced from the gap that remains when five regular tetrahedra share a common edge (Figure 2.3a). Consequently, structures which involve only negative disclinations, or an excess of them, are more common amongst the low $\rho_0$ global minima.

To calculate the network of disclination lines in a structure, one must first partition space according to the Voronoi procedure, in which each point in space is assigned to the Voronoi polyhedron of the atom to which it is closest. This allows nearest neighbours to be defined as those atoms whose Voronoi polyhedra share a face. The Delaunay network that results from joining all such nearest neighbours is the dual of the Voronoi construction and divides all space into tetrahedra. This definition of a nearest neighbour has been termed geometric, rather than physical (e.g. using a cutoff distance), and the division of space into tetrahedra that this method achieves is artificial in the sense that it is independent of whether a polytetrahedral description is appropriate. In practice we determined the Voronoi polyhedra by using the fact that a set of four atoms constitutes a Delaunay tetrahedron if the sphere that touches all four atoms contains no other atoms[105]. The centre of this sphere is then a vertex of the Voronoi polyhedron of each atom. As the number of tetrahedra around a nearest-neighbour bond is the same as the number of sides on the face common to the Voronoi polyhedra of both nearest neighbours, disclination lines can then be assigned. However, problems can occur in assigning the Delaunay network if there are more than four atoms exactly on the surface of the sphere. Such a degeneracy, which only occurs as a result of symmetry, renders the analysis non-unique. This is the case for the 55-atom Mackay icosahedra and for bulk close-packed solids because of the presence of octahedra, but is not a problem here since we only apply the method to clusters that are polytetrahedral in character. One further consideration is that the analysis should not be applied to nearest-neighbour bonds between the surface atoms of a cluster.

**Figure 2.18:** Global minima at low values of $\rho_0$ for $N\ge 38$ .If appropriate, the disclination network is displayed next to each structure. $-72^\circ$ disclinations are represented by red lines, and $+72^\circ$ disclinations by blue lines. $-144^\circ$ disclinations by green lines, and $+144^\circ$ disclinations by yellow lines.
$\begin{figure} \vspace{-0.8cm} \epsfxsize=15cm \centerline{\epsffile{s.dis1.eps}} \vspace{-1cm}\end{figure}$

**Figure 2.18:** continued.
$\begin{figure} \vspace{-0.8cm} \epsfxsize=15cm \centerline{\epsffile{s.dis2.eps}} \vspace{-1cm}\end{figure}$

The smallest global minimum that involves a disclination line is 11A. It involves a central atom surrounded by a 10-atom coordination shell, which has the structure of the hollow cluster 10A. The encapsulation of the central atom gives the structure a larger n_nn than the incomplete icosahedron 11B, but results in a larger strain energy (Table 2.2); the surface is in tension. The structure involves a single positive disclination line running through the centre of the cluster. Similarly, for N=12 and 14-16 structures with a single coordination shell become lower in energy than structures based on the icosahedron at long range. For those with N>13 the surface is in compression. As we shall see in §4.4, structures 11A, 12A, 14A, 15A and 16A correspond to Kasper polyhedra. Of these structures 15A is the most stable as measured by the range of $\rho_0$ for which it is the global minimum. For 17A, the surface has the same structure as 16A, but there are two atoms in the centre of the cluster. The second lowest energy structure of 17 at $\rho_0=3$ has a 16-coordinate central atom, which is the node for a tetrahedral array of disclinations. Structures with a more highly coordinated central atom involve increasingly large strains, and for 18, say, would only have the same n_nn as the icosahedral 18B.

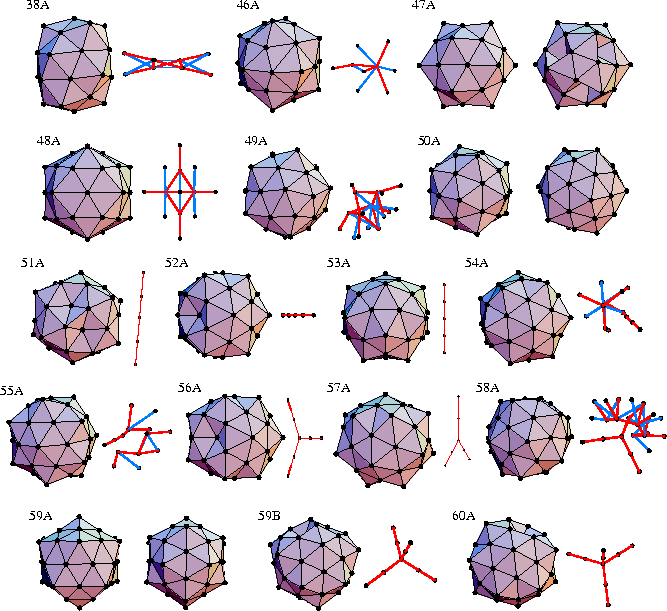
The structures 11A, 12A, 14A, 15A and 16A are all deltahedral, and so growth can occur on these structures in `anti-Mackay' or `Mackay' sites (Figure 2.9), in the same way as for the icosahedron 13A. However, if one considers the addition of a hexagonal pyramidal cap to the most stable of the Kasper polyhedra, 15A, the result is a D_6h structure with a positive disclination running the length of the symmetry axis (a disclinated equivalent of the double icosahedron 19A) that has only the same n_nn as the icosahedral structure 22A. Disclinated polytetrahedral structures cannot compete with the disclination-free polytetrahedral structures produced by the anti-Mackay overlayer to the icosahedron. Only once this growth sequence is completed at N=45 are structures with disclinations again global minima (Figure 2.18). The one exception is structure 38A, which is similar to the icosahedral structures 38B and 38C, but has two positive disclinations running through the structure in a strange double helical twist.

The most stable disclinated polytetrahedral structures occur at N=53, 57, and 61 (Figure 2.6). These are the sizes for which `anti-Mackay' overlayers of 15A, 16A and the 17-atom structure involving a tetrahedral arrangement of disclinations are completed. In these structures, those interior atoms not lying on a disclination line are icosahedrally coordinated. Many other minima are related to these stable structures: 51A and 52A are based on 53A but with missing vertex atoms; similarly, 59B and 60A are based on 61A; and 70A and 74A are based on 57A and 61A, respectively, but with an additional 13-atom cap which extends one of the `arms' of the disclination network. Furthermore, many of the other structures include parts of the disclination networks of 53A, 57A and 61A, but combined with a more disordered array of disclinations in another part of the cluster.

Other interesting structures are also seen. 47A, 50A and 59A seem to have a mixture of Mackay and anti-Mackay overlayers present. 64A is formed from the rhombic tricontahedron 45A by the extension of the structure along a three-fold axis and the addition of a ring of atoms in the centre of the cluster. However, for the larger clusters it becomes harder to recognize any motifs in the structures, and some just seem to be disordered tangles of disclinations. Disordered polytetrahedral structures involving a network of disclination lines will be considered further when the structure of liquids is discussed in detail in §4.4. It suffices to note here that the nearest-neighbour peak in the radial distribution function of these structures is broader than for the ordered structures considered in the preceding sections, and that, furthermore, these clusters when reoptimized to larger values of $\rho_0$ correlate with structures that are in the lower energy range of the band of minima associated with the liquid-like state of clusters. It is interesting that theoretical studies of sodium clusters have shown that amorphous structures are lower in energy than regular structures up to at least 340 atoms, the largest size considered in that study[106]. The present results allow us to identify the cause of these disordered structures as the relatively long range of the sodium potential.

Since most minima in this structural class do not have a common lattice, or packing scheme, it is difficult to predict the low energy structures, and so most have been found by one of the global optimization methods mentioned in §2.2.2. Fortunately, these methods are most likely to succeed at long range because the PES is smoother and has fewer minima than at shorter ranges. Another consequence of the lack of lattice structure is that the differentiation between nearest neighbours and next-nearest neighbours becomes ambiguous and the decomposition of equation 2.2 more arbitrary. For these clusters, we choose to define n_nn using a cutoff at $\rho_0$ =4 which corresponds to the distance at which the pair energy is $0.6\,\epsilon$ .