 |
 |
The energy profiles for typical low temperature quenches in minima space performed
from random starting configurations are shown in Figure 6.7
for the three clusters.
The quenches for the 13-atom cluster typically find the icosahedral
global minimum in three or four accepted steps.
This is not surprising given the relative simplicity of the PES;
the number of minima on the surface[162] is probably of the order of 1500
and none of the minima are more than four steps away from
the global minimum.![[*]](foot_motif.gif)
The quenches for 55 also find the global minimum, although the pathway and the number of steps is inevitably larger because of the increased system size. Still it is a remarkable feature of this PES that the global minimum is so easy to find considering there are probably of the order of 1021 minima on the PES. In the last part of the pathway shown in Figure 6.7c the cluster finds the Mackay icosahedron in two steps from a low energy liquid-like minimum, rather than by passing through defective Mackay icosahedra as was observed for some of the other pathways.
For LJ38 the system never finds the fcc global minimum but instead the quenches always lead into the basin of icosahedral minima and down to the lowest energy icosahedral minimum (structure 38E of Chapter 2). Although this represents a failure of the method as a global optimization tool, it provides us with some interesting information about the topography of the PES. It seems that the basin containing the icosahedral minima is much more easily accessed from higher energy minima than the basin leading down to the fcc minima. This is probably a result of the greater structural similarity between the icosahedral structures and the liquid that we discussed in §4.4.
 |
One difference between the quench pathway for LJ38 and
that of the other two clusters is that in the last stages of the
pathway the system has to search through the low energy icosahedral
isomers.
The bottom of the icosahedral basin is flatter than for LJ13
and 55, both of which have global minima that are significantly
lower in energy than the next lowest energy minimum,
making the last stages of global optimization easier.
For comparison, the energy gaps between the lowest energy icosahedral
minima are ![]() ,
, ![]() and
and ![]() for LJ13, LJ38 and 55, respectively.
for LJ13, LJ38 and 55, respectively.
As for M75 at ![]() =6 (§2.4), it may be that the 38-atom truncated
octahedron is the free energy global minimum only at low temperature.
If this is the case, we would expect a high temperature Monte
Carlo walk in minima space starting from the truncated octahedron
to escape from the fcc basin and pass into the icosahedral basin,
and this is indeed what we observed.
The length of the initial pathway between the two lowest
energy structures produced by this method was about
=6 (§2.4), it may be that the 38-atom truncated
octahedron is the free energy global minimum only at low temperature.
If this is the case, we would expect a high temperature Monte
Carlo walk in minima space starting from the truncated octahedron
to escape from the fcc basin and pass into the icosahedral basin,
and this is indeed what we observed.
The length of the initial pathway between the two lowest
energy structures produced by this method was about ![]() .
However, by performing quenches on either side of the barrier,
the pathway was significantly shortened.
The resulting pathway is illustrated in Figures 6.8 and 6.9.
The LJ38 PES clearly has similarities to some of the multiple funnels scenarios
considered in §5.4.4. From the cross-section (Figure 6.9)
it does appear that the basin surrounding the truncated octahedron is narrower than the
icosahedral basin, which is what would be expected given the propensity for LJ38 to
go into the icosahedral basin on relaxation.
.
However, by performing quenches on either side of the barrier,
the pathway was significantly shortened.
The resulting pathway is illustrated in Figures 6.8 and 6.9.
The LJ38 PES clearly has similarities to some of the multiple funnels scenarios
considered in §5.4.4. From the cross-section (Figure 6.9)
it does appear that the basin surrounding the truncated octahedron is narrower than the
icosahedral basin, which is what would be expected given the propensity for LJ38 to
go into the icosahedral basin on relaxation.
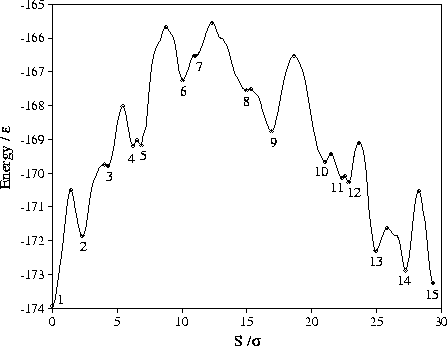 |
In the structural transformation the truncated octahedron initially undergoes
a series of rearrangements that take it to the high energy hexagonal close-packed minimum 6.
This structure then collapses to a polytetrahedral structure
typical of the liquid-like state,
which becomes more and more ordered until
it reaches the decahedral structure 11.
After two localized rearrangements, the decahedral minimum 13
is then converted to an icosahedral minimum by a multiple square-diamond process in which
one half of the structure is rotated by ![]() about the decahedral axis.
about the decahedral axis.
In electron microscopy studies of metal clusters supported on a surface, transformations are often observed between icosahedral, decahedral and fcc structures[1]. The pathway we have found here, although for a cluster much smaller than those observed experimentally, is probably fairly typical of the complex series of rearrangements and high energy barriers that need to be overcome to move between ordered structures with different morphologies.