Multiple funnels

A schematic picture of the modified PES which we have investigated is shown in Figure 5.9. It has a secondary funnel joined to the primary funnel at l=l_node. The levels in the secondary funnel are denoted by l' and have the same properties as the corresponding levels for the standard PES. Initially, we consider the case where the secondary funnel ends at l'=2', since for this case the secondary funnel hardly affects the equilibrium thermodynamics--the P_l'^eq never have significant magnitudes (see e.g. Figure 5.2c).

**Figure 5.10:** (a) Landau entropy profiles for a PES with two funnels and l_node=6. The lines are labelled by the corresponding values of the energy. The dashed lines are for the secondary funnel and points have been marked by the appropriate value of l'. (b) The energy dependence of the magnitude of the Landau entropy bottleneck for passage from the bottom of the secondary funnel to the primary funnel.
$\begin{figure} \epsfxsize=15cm \centerline{\epsffile{m.land-multi.eps}}\end{figure}$

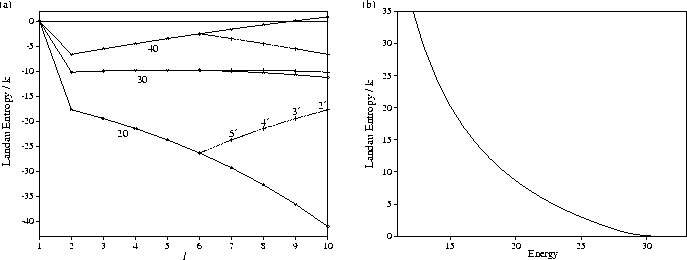
The rate of relaxation to the global minimum is not significantly affected by the secondary funnel at energies near to E_f, but as the energy is decreased the rate slows dramatically compared to the standard PES (Figure 5.9b). The latter effect becomes more pronounced at larger values of l_node. This behaviour can be explained by examining the Landau entropy (Figure 5.10). At higher energies, the bottom of the secondary funnel is not an entropy maximum, and so the system never gets trapped there. However, below the energy for which relaxation down the primary funnel is thermodynamically favourable, level l'=2' becomes a Landau entropy maximum and there is a Landau entropy bottleneck which must be overcome in passing from the secondary to the primary funnel (Figure 5.10b). The conditions which are thermodynamically most favourable for folding for the standard PES also most favour trapping in the secondary funnel.

**Figure 5.11:** (a) and (b) Time evolution of the probabilities, P_l, and (c) and (d) equilibration trees at an energy of (a) and (c) 21; and (b) and (d) 26.41 for a PES with two funnels and l_node=6. The secondary funnel ends at l'=2. Initially, *P₁₀*=1. The lines of the equilibration trees corresponding to individual levels are labelled by the appropriate values of l or l'.
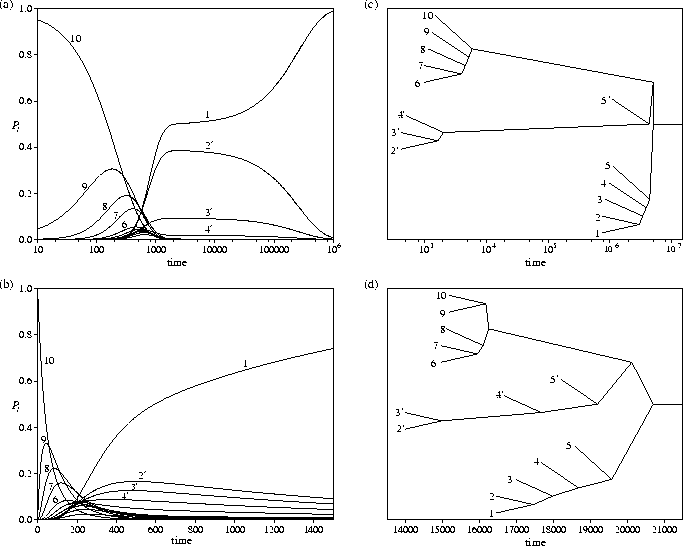$\begin{figure} \epsfxsize=15cm \centerline{\epsffile{m.ptree-multi.eps}}\end{figure}$

The consequences of these changes in the Landau entropy can be seen in the probability flows and the equilibration trees (Figure 5.11). At E=26.41, there is only a small entropy bottleneck associated with exit from the secondary funnel, and the time scale for this process is only about an order of magnitude larger than that for relaxation from high energy minima. At higher energies, where there is no entropy bottleneck, this time scale separation disappears altogether. 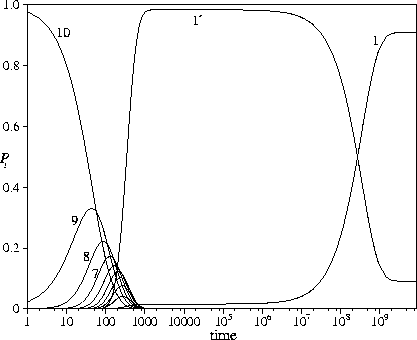However, for E=21 there is a much larger entropy bottleneck to be overcome. By t=1000, the system has relaxed down the PES, reaching a state where $P_1\approx \half$ and the probability of being in the secondary funnel is also close to a half (Figure 5.11a). In the initial relaxation the system is equally likely to go into either funnel, because both funnels have the same properties around l=l_node. This situation persists for about two orders of magnitude in time (note the log scale in the figure) until the probability begins to flow from the secondary funnel into the primary. The same basic structure is seen for both equilibration trees in Figure 5.11; equilibration occurs separately above l_node and within the bottoms of the two funnels. The tree for E=21 clearly shows the large separation in time scales.

There have been some interesting investigations of the effects of trapping by low energy non-native states in protein folding simulations[262,273]. These show that at low temperatures there is a fast component to the relaxation rate, which corresponds to the protein passing directly into the native structure, and a slower component, where the system becomes trapped in one of the low energy non-native states before reaching the native structure. As for our model PES, this separation of time scales can disappear at higher temperatures[262]. Experimental studies of protein folding often show kinetics with two (or more) time scales present[264,274,275,276,277,278]; there are subpopulations of proteins which fold at different rates. Experiments on hen lysozyme have clearly shown that the faster rate corresponds to direct folding to the native state[276], and it has been inferred that the slower rate is due to trapping in low energy non-native structures. This interpretation has been confirmed for cytochrome c. For this protein, the chain misorganization responsible for trapping is the incorrect ligation of a haem group by a histidine residue. Under refolding conditions which prevent this incorrect contact forming, the protein folds on a time scale of 15ms, but when trapping occurs folding takes longer than 0.3s[278]. The temperature dependence of the two rate constants[264] for cytochrome c agrees well with the behaviour of our model PES. The faster rate constant exhibits a maximum, as would be expected for direct relaxation to the global minimum (Figure 5.3a), whereas the rate constant for the slower process just decreases as the temperature decreases[264], which is what would be expected when the magnitude of the Landau entropy bottleneck for escape from a trap increases with decreasing temperature (Figure 5.10b).

Interestingly, it has been suggested that chaperonins, such as GroEL and GroES, assist protein folding by reducing the effect of trapping[279,280]. The chaperonins bind proteins which are trapped in non-native structures and then release them in a less folded state, thus allowing the protein another opportunity to find the native structure directly. Simulations show that the folding rate of slow-folding proteins increases significantly when this `iterative annealing' model for chaperonin action is included[281], lending further credence to this proposal.

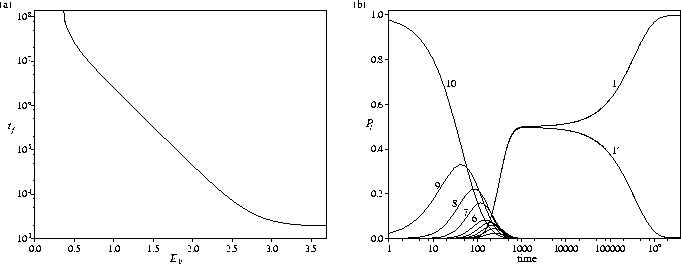
The trapping properties of the secondary funnel can be increased by adding a minimum at l'=1', as shown in Figure 5.12a. t_f increases exponentially as the depth of the secondary funnel is increased. As E_1' approaches the value for which P_1'^eq=0.2 (E_1'=0.364), t_f increases even more rapidly, as expected from our definition of t_f (P₁(t_f)=0.8). At higher energies, the dependence of the relaxation rate on E_1' diminishes as E_2' is approached. For this system the probability density flows rapidly and equally into the bottoms of both funnels and then begins to trickle very slowly back up the PES from l'=1' into the primary funnel (Figure 5.12b). This PES provides an example where the energy difference between the two lowest energy minima has a very significant effect on the relaxation rate to the global minimum, and supports our suggestion that this quantity is most important when the two minima equilibrate very slowly because they are structurally dissimilar and well-separated on the PES.

The PES of (KCl)₃₂ shows some interesting features. The relaxation down to the low energy rock-salt-like structures from the amorphous states is rapid[91]. However, it is not clear whether the system can then reach the ( $4\times4\times4$ ) global minimum from the other rock-salt-like structures, which can have very different shapes from the global minimum, e.g. the second lowest energy minimum has a ( $5\times4\times3$ ) shape plus an extra row of four atoms[127]. It might be that these crystal-like structures have separate funnels, the steep slopes of which make interconversion to other rock-salt-like structures difficult. This would give rise to a significant separation between time scales for relaxation down the PES and equilibration between the rock-salt-like structures, similar to that seen for our model PES above.

**Figure 5.12:** Dynamic properties of a PES with two funnels and l_node=6 at an energy of 26.41. The secondary funnel ends at l'=1. (a) Dependence of t_f upon *E_1'*. (b) Time evolution of the probabilities, P_l, for *E_1'*=1.5 from an initial distribution *P₁₀*=1.
$\begin{figure} \epsfxsize=15cm \centerline{\epsffile{m.trap.eps}}\end{figure}$

In the above examples, the properties of both funnels were the same except at l'=1'. As a result, the initial relaxation down the PES was equally likely to take the system into either funnel. However, for materials that easily form glasses the system is more likely to relax into the amorphous glassy minima than into the crystalline minima. A similar effect can be achieved in our model by making the `width' of the primary funnel narrower than that of the secondary. g determines the number of minima in each level, and consequently also determines the increase in the configurational entropy as the funnel is ascended, i.e. its width. Therefore, if we make the value of g for the primary funnel below l_node, g_p, where g_p is smaller than for the rest of the PES, the primary funnel is only connected to g_p^l_node-1 of the g^l_node-1 minima in the level l=l_node. For the parameters l_node=6, g_p=4 and g=10, this corresponds to only 1% of the minima in the level l=l_node. These changes to the PES affect the rate of transition between levels l_node and l_node-1, which becomes

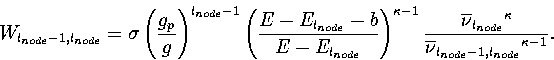$\begin{displaymath} W_{l_{node}-1,l_{node}}= \sigma \left({g_p\over g}\right)^{l... ...}}^\kappa\over{\overline\nu_{l_{node}-1,l_{node}}}^{\kappa-1}}.\end{displaymath}$

(5.14)

This PES can mimic some of the effects of frustration. If, as in simple liquids, the high potential energy amorphous minima have a different type of order from the crystalline global minimum, one might expect that the glassy states at the bottom of the liquid-like band of minima maximize the polytetrahedral order as far as is possible. Therefore, the glassy minima are not likely to be connected to the crystalline funnel, but instead reside at the bottom of rugged funnels which descend from the liquid-like regions of configuration space. In contrast, the funnel terminating at the crystalline state is likely to be connected to a small fraction of the higher energy amorphous minima which contain incipient crystal-like nuclei. Consistent with this idea, large Landau free energy barriers have been found in simulations of nucleation of a crystalline phase from a Lennard-Jones liquid[269,270]. This view of the PES topography of glass-formers has many similarities to the ideas put forward by Stillinger for fragile liquids[271,272].

**Figure 5.13:** Dynamic properties of a PES with two funnels and l_node=6. For l<l_node the primary funnel has a lower value of g than for the rest of the PES. The secondary funnel ends at l'=2. (a) Dependence of t_f upon g_p at an energy of 26.41. (b) Landau entropy profiles when g_p=4 at different values of the energy as labelled. (c) Time evolution of the probabilities, P_l, and (d) Equilibration tree when g_p=4 from an initial distribution *P₁₀*=1 at an energy of 26.41.
$\begin{figure} \epsfxsize=15cm \centerline{\epsffile{m.frus.eps}}\end{figure}$

We now choose to end the secondary funnel at l'=2' since glasses normally have a significantly higher potential energy than the crystalline state. For this PES, the rate of relaxation to the global minimum dramatically slows as the primary funnel is narrowed by decreasing g_p (Figure 5.13a). This occurs because the level l=5 has a lower entropy than l'=5' and l_node=6 (Figure 5.13b). On reaching l=l_node, the system is much more likely to pass into the secondary funnel, rather than overcome the Landau entropy bottleneck associated with passage into the primary funnel. The depth of this bottleneck increases as the width of the primary funnel decreases.

The time evolution of the probabilities when g_p=4 shows that all the probability initially passes into the secondary funnel, and then slowly trickles back through the Landau entropy bottleneck into the global minimum (Figure 5.13c). This results in a large separation of time scales between the time for equilibration within the secondary funnel and between the two funnels (Figure 5.13d).

This example shows that the secondary funnel is a more effective trap when it has a larger width than the primary funnel. Earlier in this section, we showed that a low energy minimum at the bottom of the secondary funnel also increases its trapping efficiency. By combining these two features we can create a PES where virtually all the probability flows to the bottom of the secondary funnel, and then remains there for a long time (Figure 5.14). Only on very long time scales does the global minimum start to become significantly populated; t_f for this PES is $7.4\times 10^8$ .In the example shown E_1'=0.6, and so P_1'^eq=0.091, thus preventing complete population of the global minimum at the total energy considered. This PES provides an example of how relaxation to a unique metastable minimum might occur, simply because of its greater kinetic accessibility. A similar behaviour is seen for some proteins from the serpin family of protease inhibitors[282]; the protein plasminogen activator inhibitor-1 first folds to the active state, but then on a time scale of hours can spontaneously transform to an inactive latent form[154,283].

**Figure 5.14:** Time evolution of the probabilities, P_l, for a PES with two funnels and l_node=6 at a total energy of 26.41. For l<l_node the primary funnel has g_p=4. The secondary funnel ends at l'=1 at a potential energy *E_1'*=0.6. Initially, *P₁₀*=1.
$\begin{figure} \epsfxsize=10cm \centerline{\epsffile{m.ftrap.eps}}\end{figure}$

The above PES bears some resemblance to the 38-atom and 75-atom Lennard-Jones clusters, for which the low energy icosahedral minima are reached on relaxation down the PES, rather than the fcc or decahedral global minimum[73,89]. The difficulty in reaching the global minima is associated with the narrowness of the funnels leading down to the global minima. Our results also suggest that it would not be so surprising if it was effectively impossible to reach the global minimum of the 75-atom cluster by a dynamic method without biasing the system towards decahedral minima. These clusters, though, have an additional complication compared to our model PES. The free energy global minimum depends on temperature, and only at low temperatures does it actually correspond to the global potential energy minimum. This is because of the greater configurational entropy of the minima at the bottom of the icosahedral funnel (§2.4).