Correlation Diagrams

 

  

Figure 4.3: Probability distributions of the potential energy for samples of minima of M₁₃, M₅₅, M₁₄₇ and bulk material. The samples contain 131, 858, 298 and 117 minima, respectively. Some of the peaks are labelled with the structures they correspond to. I stands for icosahedron, MI for Mackay icosahedron, + nd for a structure with n defects.

We employed molecular dynamics and conjugate-gradient techniques to generate between 10² and 10³ local minima for each PES at $\rho_0=6$.The simulations of bulk material were performed at constant volume in a cubic box containing 256 atoms at a reduced density of $\sqrt 2$. The three clusters we studied contained 13, 55 and 147 atoms, and have been chosen because they correspond to sizes for which complete Mackay icosahedra are possible. In the melting region these clusters fluctuate between a solid-like and a liquid-like state as a function of time. Consequently, a simulation at a single energy in this coexistence region was sufficient to sample all relevant regions of the PES's of the M₁₃ and M₅₅ clusters. However, for M₁₄₇ separate simulations were needed to sample the equilibria between the solid and its low energy defective states, and between the high energy defective states of the solid and the liquid.

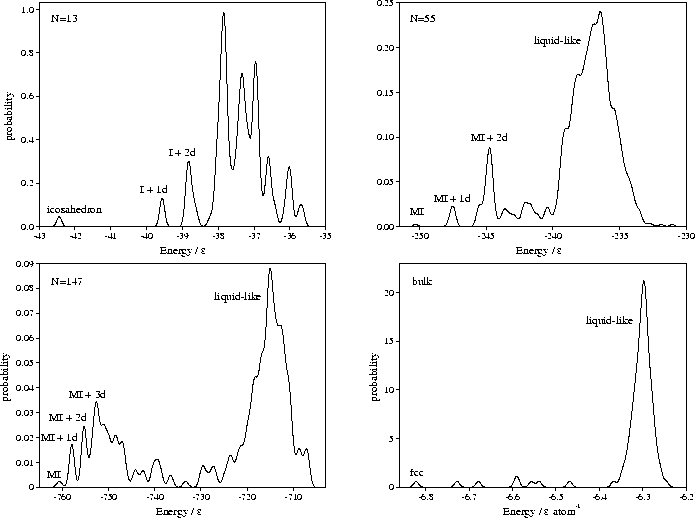
The four distributions of minima obtained are shown in Figure 4.3. The geometries of the local minima were subsequently reoptimized for ascending and descending integer values of $\rho_0$. For the bulk material, the box size was scaled at each value of $\rho_0$ to keep the energy of the fcc minimum at a constant fraction of its zero-pressure energy. On changing $\rho_0$ a minimum may disappear from the PES. When this occurs, geometry optimization leads to a new minimum and this causes the discontinuities in the correlation diagrams (Figure 4.4). This effect is particularly noticeable for the 13-atom cluster at long range, because the total number of minima on the PES at $\rho_0$=3 is less than the number of minima in our sample from $\rho_0$=6 (Table 2.1).

  

Figure 4.4: Correlation diagrams for M₁₃, M₅₅, M₁₄₇ and bulk material. In each case the unit of energy is the binding energy of the lowest energy fcc structure. The samples contain 131, 858, 298 and 117 minima, respectively. Lines due to the decahedral and fcc structures which become the global minimum at large values of $\rho_0$ for M₅₅ and M₁₄₇ and the amorphous structure which is the global minimum of M₁₄₇ at $\rho_0$=3 have been added.

 

The lowest energy line in each correlation diagram at any given $\rho_0$ corresponds to the solid phase, since at zero Kelvin this structure must have the lowest free energy. For the bulk material (Figure 4.4), the lowest energy minimum is fcc for all values of $\rho_0$. However, as we saw in Chapter 2 the structure of the global minimum depends on $\rho_0$ for clusters. The global minima of M₁₄₇ are illustrated in Figure 4.5, and their energies and the ranges of $\rho_0$ for which they are the global minima are given in Table 4.1.

  

Figure 4.5: Global minima for M₁₄₇. Each structure is labelled by the symbol given in Table 4.1.

3pt

 

$$E_{\rm strain} \rho_0=3.0 \rho_0=6 \rho_0=10 \rho_0=14 \rho_{min} \rho_{max}$$ PG n_nn

147A C₁ 729 97.629 -1531.499 -732.549 -637.693 -605.600 3.56

147B I_h 696 26.896 -1509.272 -760.631 -678.171 -644.002 3.56 9.12

147C C_s 674 1.514 -748.869 -682.399 -672.885 9.12 10.91

147D C_s 674 1.495 -748.598 -682.386 -672.911 10.91 18.88 147E

In the correlation diagrams the relative slope of two lines is a measure of the difference in strain energies between two minima, a more positive slope implying a larger strain energy. For bulk material, the lowest energy lines above the fcc minimum are either close-packed structures misoriented with respect to the cubic box, or are based on the fcc minimum and contain defects such as vacancy-interstitial pairs. Both types of structure have a positive slope with respect to the perfect fcc structure, in the first case because the structure has to be sheared in order to fit into the box, and in the latter case because the interstitial defects introduce local strains. Although vacancies could be accommodated without any strain, the constant number and volume constraints used in this study only allow defects to be generated in pairs.

In contrast, the low energy lines in the cluster correlation diagrams run parallel to the line due to the icosahedral global minimum--a sign of their structural similarity. These lines are due to icosahedra with vacancies in the surface layer and adatoms on the surface. These minima give rise to the roughly equally-spaced peaks in the low energy region of the M₅₅ and M₁₄₇ probability distributions in Figure 4.3, and correspond to increasing numbers of defects. Rearrangements between these structures occur at energies just below that required for complete melting, leading to enhanced diffusion in the surface layer[110,111].

  

Figure 4.6: Plots of the strain energy versus the potential energy for the samples of $\rho_0$=6 minima for M₁₃, M₅₅, M₁₄₇ and bulk material. The sample of M₁₃ minima is larger than that used in Figure 4.4 and contains 1441 minima (Table 2.1).

The thick bands of lines with positive slope in the bulk, M₅₅ and M₁₄₇ correlation diagrams along with the corresponding large, high energy peaks in the potential energy distributions (Figure 4.3) are due to minima found by quenching from the region of phase space corresponding to liquid behaviour. We have sampled only a tiny fraction of all these `liquid-like' minima; for comparison, the number of minima corresponding to the liquid-like phase space of M<sub>55</sub> has been estimated as $8.3\times10^{11}$ (§3.6). It is because of this large configurational entropy and the greater vibrational entropy that the free energy of the liquid phase usually becomes lower than that of the solid phase as the temperature increases, leading to melting. For the bulk, the energy gap between these `liquid-like' minima and the fcc minimum clearly increases with $\rho_0$ (Figure 4.4). Thus, decreasing the range of the potential energetically destabilizes the liquid phase. For the clusters the energy of the `liquid-like' minima must be compared to the energy of the global minimum. As the decahedral and fcc structures which become global minima at short range were not obtained in the sample of minima at $\rho_0$=6, the lines due to these structures have been added to the correlation diagrams, although we have not added lines due to the many defective minima based upon them. Hence, a similar result to bulk is seen for M<sub>55</sub> and M<sub>147</sub>, i.e. the energy gap between the `liquid-like' minima and the lowest energy solid structure, be it icosahedral or decahedral, clearly increases as the range decreases (Figure 4.4).

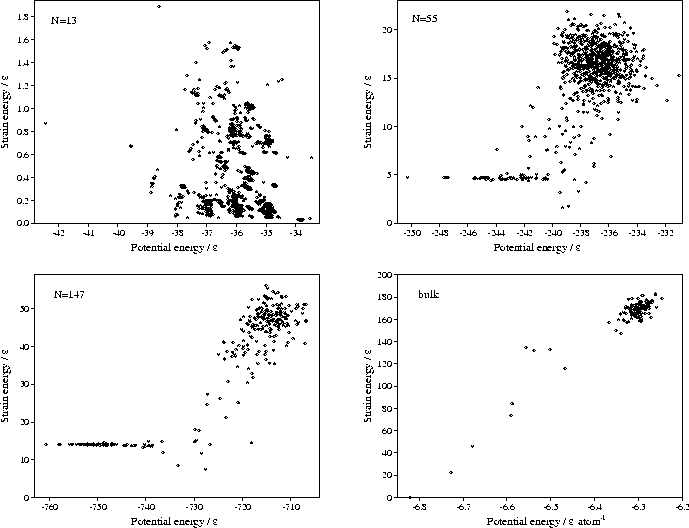
The physical basis for this behaviour is simply the greater strain energy of the `liquid-like' minima, as shown by their positive slope in the correlation diagrams. Figure 4.6 shows clearly the differentiation between the low potential energy, low strain energy minima and the high potential energy, high strain energy `liquid-like' minima. This greater strain arises from the inherent disorder of the `liquid-like' minima; they have a range of nearest-neighbour distances, and consequently the first peak in the radial distribution function is broader than for the solid. The strain energy is the energetic penalty for this disorder and it rises rapidly as the range decreases and the potential wells narrow. 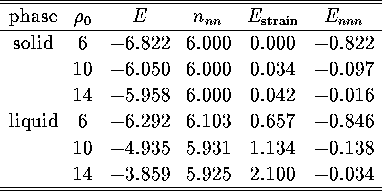This view is confirmed by examining the three contributions to the energy for the two bulk phases at different values of $\rho_0$ (Table 4.2). The main contribution to the energy gap is found to be the larger strain energy of the liquid minima. This greater strain energy will be related to the liquid structure in more detail in §4.4.

  

Table 4.2: Partitioning of the potential energy of the bulk phases into the different contributions of equation 2.1 at different values of $\rho_0$. The values for the liquid phase are averages over all the `liquid-like' minima. All energies are given in reduced units per atom. The nearest-neighbour criterion, x₀=0.243, corresponds to the minimum between the first and second peaks of the radial distribution function.

The energetic destabilization of the liquid phase seen for bulk and the two larger clusters gives rise to a term in the free energy difference between the solid and liquid phases which increases rapidly with $\rho_0$. Since the energetics of the vapour phase can be assumed to be relatively unaffected by the range of the potential, the rise in energy of the `liquid-like' minima with $\rho_0$ for bulk and the two larger clusters also causes the energy difference between the liquid and vapour to decrease. Thus, the range-dependence of the energetics should have a large effect on the free energy differences both between the solid and liquid phases and between the liquid and vapour phases, in both cases destabilizing the liquid phase. It is significantly harder to determine the range-dependence of the entropic contribution to the free energy in our approach. However, the entropy of the vapour phase should be relatively unaffected by $\rho_0$ and the entropy of both the solid and the liquid phases decreases as $\rho_0$ increases due to the narrowing of the potential wells and the attendant loss of accessible configuration space. We have shown that the range-dependence of the energetics is sufficient to account for the known range-dependence of the phase diagram and in particular the decrease of the critical temperature as the potential becomes more short-ranged. Thus, at least part of the destabilization of the liquid phase that has been noted in experiments and simulations of colloids and can be traced to the PES in this way.

The situation for M₁₃ is rather different because of its small size--this cluster is nearer to the atomic limit. The introduction of defects in the icosahedron involves an increase in the energy of the cluster which is a significant fraction of the total potential energy. The heat capacity peak found for LJ₁₃ (it should exhibit very similar behaviour to an M₁₃ cluster with $\rho_0=6$) is associated with isomerization between the icosahedron and the defective structures based upon it[128], rather than between two phase-like forms that are structurally dissimilar. The nature of the `melting' transition is therefore significantly different from the larger clusters and from bulk. As the removal of an atom from the vertex of the icosahedron allows relaxation of some of the strain, the gap between the icosahedron and the defective states decreases as the range of the potential decreases.

There is another interesting effect evident in the correlation diagrams of M₅₅ and M₁₄₇: as $\rho_0$ decreases the gap between the `liquid-like' band of minima and the Mackay icosahedron decreases until for a sufficiently long-ranged potential the `liquid-like' band becomes lower in energy than the icosahedron. At $\rho_0=3$ for both M₅₅ and M₁₄₇, the lowest energy clusters (55A and 147A) have an amorphous structure typical of the liquid-like state, which as we saw in §2.3.4 can be analysed in terms of disclination lines.