


Next: Traversing the Potential Energy
Up: Characterizing the Topography of
Previous: Characterizing the Topography of
Home: Return to my homepage
As the dynamical behaviour of a system is determined by the PES,
characterization of the topography and topology of the PES is
a prerequisite for understanding the dynamics.
For example, to apply the master equation approach that we used for our model
PES's in the previous chapter, one would need a complete sample
of minima and transition states on the PES.
Such sampling is only possible for very small clusters (up to 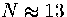 ) because of
the exponential increase in the number of minima with size[64,65,162].
For larger clusters one would need some way to statistically characterize the PES in
order to compensate for the incompleteness of any sample of stationary points.
This would be akin to the method we used in §3.4 to reproduce the
thermodynamics from an incomplete sample of minima.
) because of
the exponential increase in the number of minima with size[64,65,162].
For larger clusters one would need some way to statistically characterize the PES in
order to compensate for the incompleteness of any sample of stationary points.
This would be akin to the method we used in §3.4 to reproduce the
thermodynamics from an incomplete sample of minima.
Here we use the eigenvector-following method to obtain a comprehensive
characterization of the M13 PES and its dependence on the range parameter,
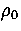 (§6.3),
and to provide some typical downhill pathways for LJ clusters (§6.4).
These surveys of the PES allow qualitative predictions of the effects of the
range on the dynamics, and insight into the known relaxation behaviour of LJ clusters.
Quantitative predictions await the application of the master equation method.
(§6.3),
and to provide some typical downhill pathways for LJ clusters (§6.4).
These surveys of the PES allow qualitative predictions of the effects of the
range on the dynamics, and insight into the known relaxation behaviour of LJ clusters.
Quantitative predictions await the application of the master equation method.



Next: Traversing the Potential Energy
Up: Characterizing the Topography of
Previous: Characterizing the Topography of
Jon Doye
8/27/1997
![]() (§6.3),
and to provide some typical downhill pathways for LJ clusters (§6.4).
These surveys of the PES allow qualitative predictions of the effects of the
range on the dynamics, and insight into the known relaxation behaviour of LJ clusters.
Quantitative predictions await the application of the master equation method.
(§6.3),
and to provide some typical downhill pathways for LJ clusters (§6.4).
These surveys of the PES allow qualitative predictions of the effects of the
range on the dynamics, and insight into the known relaxation behaviour of LJ clusters.
Quantitative predictions await the application of the master equation method.