


Next: Anharmonicity
Up: Thermodynamics of Small Lennard-Jones
Previous: The 55-atom Lennard-Jones Cluster
Home: Return to my homepage
The total energy density of
states associated with a single minimum on the
PES is in the harmonic approximation[161]
| 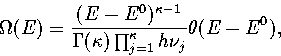 |
(3.4) |
where E0 is the potential energy of the minimum,
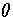 is the Heaviside step function, and
is the Heaviside step function, and 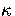 ,the number of vibrational degrees of freedom, is 3N-6.
(As we will be comparing our results to those for stationary, non-rotating clusters,
we do not include translational or rotational contributions to the density of states.)
To calculate the density of states for the whole system, all the minima on the PES need
to be considered. We make a superposition approximation and sum the
density of states over all the minima low enough in energy to contribute.
This approximation is equivalent to assuming that the phase space
hyperellipsoids associated with each minimum do not overlap.
This gives
,the number of vibrational degrees of freedom, is 3N-6.
(As we will be comparing our results to those for stationary, non-rotating clusters,
we do not include translational or rotational contributions to the density of states.)
To calculate the density of states for the whole system, all the minima on the PES need
to be considered. We make a superposition approximation and sum the
density of states over all the minima low enough in energy to contribute.
This approximation is equivalent to assuming that the phase space
hyperellipsoids associated with each minimum do not overlap.
This gives
| 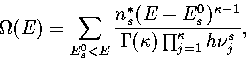 |
(3.5) |
where the sum is over all the geometrically distinct minima on the surface;
n*s, the number of permutational isomers of minimum s, is given by
ns*=2N!/hs where hs is the order of the point group of s.![[*]](foot_motif.gif)
The difficulty with equation 3.5 is that for all but the very smallest
clusters this sum involves an impractically large number of minima.
Hoare and McInnes[64], and more recently Tsai and Jordan[162] have enumerated
lower bounds to the number of geometric isomers for LJ clusters from 6 to 13 atoms.
This number rises exponentially with N.
Extrapolating this trend gives for LJ55 an estimate of 1021 geometric isomers.
In such a case, as it is not possible to obtain a
complete set of minima, a
representative sample is needed. A large
set of minima can be obtained by systematic quenching from a
high energy MD trajectory.
However, this gives a greater proportion of the low energy minima than of
the high energy minima. Consequently, if the sample is used in equation 3.5 it
is likely to underestimate the density of states due to the high energy minima,
and so be inaccurate at high energies.
A method is needed which corrects for the incomplete nature of the sample of minima.
This correction can be achieved by weighting the density of states for each known minimum
by gs, the number of minima of energy E0s for which the minimum s is representative.
Hence,
| 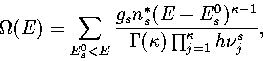 |
(3.6) |
where the sum is now over a representative sample of minima.
The effect of gs can be incorporated by using the quench statistics.
If the system is ergodic and the MD run is performed at constant energy,
the number of quenches to a minimum, 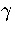 , is assumed to be proportional to the
density of states of the set of gs minima, i.e.
, is assumed to be proportional to the
density of states of the set of gs minima, i.e. 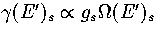 .
Hence,
.
Hence,
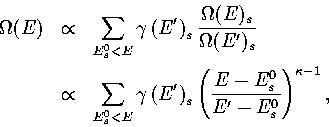
(3.7)
(3.8)
where E' is the energy of the MD run.
This reweighting technique is analogous to histogram Monte Carlo,
but instead of determining the configurational density of states from the canonical potential energy
distribution, g, effectively a density of minima, is found from the microcanonical probability
distribution for quenching to a minimum.
If all the low energy minima are known, the n* formula (equation 3.5)
will be accurate at low energies.
Therefore, the proportionality constant in the above equation can be found
by matching it to the low energy form of the n* formula. For LJ13 and
LJ55, the term due to the icosahedron is dominant at low energies, and other
terms in the sum can be neglected.
Comparing the first terms of equations 3.5 and 3.8 gives for the
proportionality constant, c
| 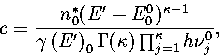 |
(3.9) |
where E00 is the energy of the global minimum.
Figure 3.5:
Microcanonical caloric curves for LJ55.
The solid lines were calculated from the 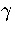 formula,
the dashed lines were calculated from the n* formula,
and the dashed line with diamonds shows the simulation results.
The sample of minima used in the calculations is marked on the graph.
formula,
the dashed lines were calculated from the n* formula,
and the dashed line with diamonds shows the simulation results.
The sample of minima used in the calculations is marked on the graph.
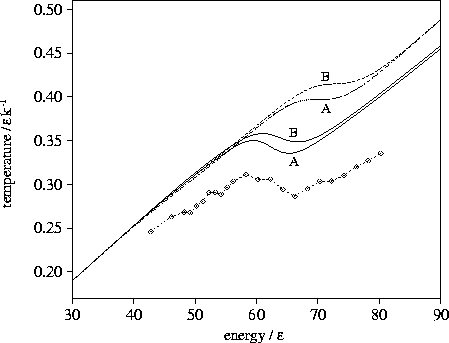 |
A critical test of these formulae for 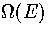 is the predicted microcanonical caloric curve,
which for LJ55 has a Van der Waals loop[135].
Using the thermodynamic definition of the microcanonical temperature,
is the predicted microcanonical caloric curve,
which for LJ55 has a Van der Waals loop[135].
Using the thermodynamic definition of the microcanonical temperature, 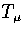 ,
,
| 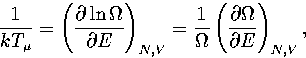 |
(3.10) |
an expression for 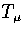 can be derived[153].
For LJ55 we have two samples of minima produced by systematic
quenching[153], details of which are given in Table 3.4.
Sample A is from a MD run at an energy in the upper end of the coexistence region,
and B at an energy just into the liquid-like region.
The results for samples A and B using the n* and
can be derived[153].
For LJ55 we have two samples of minima produced by systematic
quenching[153], details of which are given in Table 3.4.
Sample A is from a MD run at an energy in the upper end of the coexistence region,
and B at an energy just into the liquid-like region.
The results for samples A and B using the n* and 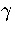 formulations
are given in Figure 3.5.
It can be seen the n* formula fails badly, predicting only
an inflection in the caloric curve which is too high in energy.
This failure is because the contribution to
formulations
are given in Figure 3.5.
It can be seen the n* formula fails badly, predicting only
an inflection in the caloric curve which is too high in energy.
This failure is because the contribution to 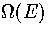 from the higher energy minima is underestimated.
The
from the higher energy minima is underestimated.
The 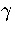 formula is much more successful, reproducing the Van der Waals loop at the observed
energy.
That the harmonic superposition method produces a
caloric curve with the correct features shows, as Bixon and Jortner suggested[152],
that the distribution of minima is crucial in determining the basic form of the caloric curve.
However, the Van der Waals loop is too shallow and lies at too high a temperature.
The discrepancy is due to the harmonic approximation. The temperature rises linearly with energy
for a single harmonic well. The actual wells of the cluster, however, are flatter than assumed in the harmonic
approximation, especially around the transition state regions.
Consequently, the cluster spends more time in these high potential energy, low
temperature regions of the PES, and so the true temperature is lower than that
given by the harmonic approximation.
formula is much more successful, reproducing the Van der Waals loop at the observed
energy.
That the harmonic superposition method produces a
caloric curve with the correct features shows, as Bixon and Jortner suggested[152],
that the distribution of minima is crucial in determining the basic form of the caloric curve.
However, the Van der Waals loop is too shallow and lies at too high a temperature.
The discrepancy is due to the harmonic approximation. The temperature rises linearly with energy
for a single harmonic well. The actual wells of the cluster, however, are flatter than assumed in the harmonic
approximation, especially around the transition state regions.
Consequently, the cluster spends more time in these high potential energy, low
temperature regions of the PES, and so the true temperature is lower than that
given by the harmonic approximation.
Table 3.4:
Details of the two samples of minima used for LJ55.
E' is measured with respect to the global minimum icosahedron.
| |
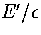 |
Number of minima
|
| A |
64.7485 |
989 |
| B |
70.2485 |
1153 |
For smaller clusters it was found that the performance of the n* formula improved[155].
This improvement occurs because there are fewer minima on the PES of a smaller
cluster and so the set of minima obtained from quenching is more complete.
The harmonic superposition method has three main possible sources of error.
The first is associated with the statistical accuracy of the quench frequencies.
These errors can be mostly eliminated by having a long enough quench run to ensure ergodicity,
and by choosing an appropriate energy for
the MD run so that the relevant regions of phase space are all significantly sampled.
When studying the thermodynamics of melting it is most appropriate to choose E' to lie in the
coexistence region, as in the case of sample A, so that quenches to solid-like and liquid-like
states are frequent.
The second possible source of error is the assumption that the
phase space volumes for each minima can be summed
independently, i.e. the hyperellipsoids in phase space do not overlap.
If overlap occurred 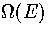 would be overestimated.
Of course, above an energy threshold the true phase space volumes of each minimum are
interconnected, but this interconnection is normally due to the anharmonic extension
of the phase volumes to form necks along the transition state valleys.
The third possible source of error is the harmonic approximation. Near the
bottom of the well this is a reasonable assumption, but as the energy is
increased some parts of the well become increasingly flat.
Consequently the harmonic approximation causes
would be overestimated.
Of course, above an energy threshold the true phase space volumes of each minimum are
interconnected, but this interconnection is normally due to the anharmonic extension
of the phase volumes to form necks along the transition state valleys.
The third possible source of error is the harmonic approximation. Near the
bottom of the well this is a reasonable assumption, but as the energy is
increased some parts of the well become increasingly flat.
Consequently the harmonic approximation causes 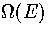 to be underestimated. Comparison of the caloric curves from simulation and the harmonic
superposition method (Figure 3.5) shows that the harmonic superposition method does indeed
underestimate
to be underestimated. Comparison of the caloric curves from simulation and the harmonic
superposition method (Figure 3.5) shows that the harmonic superposition method does indeed
underestimate 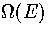 and so the harmonic approximation is likely to be the main source of
error.
and so the harmonic approximation is likely to be the main source of
error.



Next: Anharmonicity
Up: Thermodynamics of Small Lennard-Jones
Previous: The 55-atom Lennard-Jones Cluster
Home: Return to my homepage
Jon Doye
8/27/1997
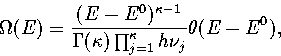
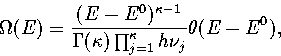
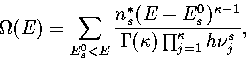
![[*]](foot_motif.gif)
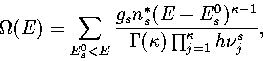
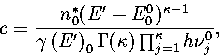

![]() is the predicted microcanonical caloric curve,
which for LJ55 has a Van der Waals loop[135].
Using the thermodynamic definition of the microcanonical temperature,
is the predicted microcanonical caloric curve,
which for LJ55 has a Van der Waals loop[135].
Using the thermodynamic definition of the microcanonical temperature, ![]() ,
,
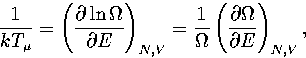
![]() would be overestimated.
Of course, above an energy threshold the true phase space volumes of each minimum are
interconnected, but this interconnection is normally due to the anharmonic extension
of the phase volumes to form necks along the transition state valleys.
The third possible source of error is the harmonic approximation. Near the
bottom of the well this is a reasonable assumption, but as the energy is
increased some parts of the well become increasingly flat.
Consequently the harmonic approximation causes
would be overestimated.
Of course, above an energy threshold the true phase space volumes of each minimum are
interconnected, but this interconnection is normally due to the anharmonic extension
of the phase volumes to form necks along the transition state valleys.
The third possible source of error is the harmonic approximation. Near the
bottom of the well this is a reasonable assumption, but as the energy is
increased some parts of the well become increasingly flat.
Consequently the harmonic approximation causes ![]() to be underestimated. Comparison of the caloric curves from simulation and the harmonic
superposition method (Figure 3.5) shows that the harmonic superposition method does indeed
underestimate
to be underestimated. Comparison of the caloric curves from simulation and the harmonic
superposition method (Figure 3.5) shows that the harmonic superposition method does indeed
underestimate ![]() and so the harmonic approximation is likely to be the main source of
error.
and so the harmonic approximation is likely to be the main source of
error.