


Next: The effect of transition
Up: Thermodynamics of Small Lennard-Jones
Previous: The Harmonic Superposition Method
Home: Return to my homepage
Most attempts to model anharmonicity
have concentrated on small systems. As
the size of the system increases the difficulty increases greatly. For example,
it would be impossible to do the necessary multi-dimensional phase space integrals in the
definition of 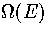 ,
,
| 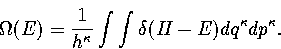 |
(3.11) |
Most approaches either attempt to calculate the anharmonic element using known
information from the PES, such as the third and fourth derivatives of the
potential at the minima and the dissociation energies[163] or assume the
PES has a certain topology for which the partition function is known[164,165].
A normal mode approximation is often used because
the multi-dimensional partition function is then the product of the one-dimensional
normal mode partition functions. However, to then obtain the density of states
the partition function must be inverse Laplace transformed. This procedure does not
necessarily have an analytic solution, and so numerical methods sometimes have
to be used[166,167].
The only attempt, that we know of, to evaluate analytically
the anharmonic density of states of clusters is due to Chekmarev and Umirzakov[165].
Their expression contained a number of unknown parameters, which they had to estimate.
This approximate approach was partly due to their lack of information about the PES
of 13, the cluster they considered.
They showed their form was able to produce the types of feature seen in the 13 caloric curve,
if not to reproduce it accurately. The approach we use here is similar.
We are looking for a relatively simple method that will provide an analytical expression
for the anharmonic contribution to 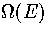 .
We also want to examine how far it is possible to use information extracted from the PES in this task.
We will focus on 55 as a test of the methods developed.
For 55 we have a sample of 3481 transition states which were found from a random selection of
402 of the minima in sample B defined above[90].
We have also calculated the analytical third derivatives for this potential.
.
We also want to examine how far it is possible to use information extracted from the PES in this task.
We will focus on 55 as a test of the methods developed.
For 55 we have a sample of 3481 transition states which were found from a random selection of
402 of the minima in sample B defined above[90].
We have also calculated the analytical third derivatives for this potential.



Next: The effect of transition
Up: Thermodynamics of Small Lennard-Jones
Previous: The Harmonic Superposition Method
Home: Return to my homepage
Jon Doye
8/27/1997
![]() .
We also want to examine how far it is possible to use information extracted from the PES in this task.
We will focus on 55 as a test of the methods developed.
For 55 we have a sample of 3481 transition states which were found from a random selection of
402 of the minima in sample B defined above[90].
We have also calculated the analytical third derivatives for this potential.
.
We also want to examine how far it is possible to use information extracted from the PES in this task.
We will focus on 55 as a test of the methods developed.
For 55 we have a sample of 3481 transition states which were found from a random selection of
402 of the minima in sample B defined above[90].
We have also calculated the analytical third derivatives for this potential.