


Next: The effect of well
Up: Anharmonicity
Previous: Anharmonicity
Home: Return to my homepage
Transition states are crucial to the dynamics of a system,
but how much effect do they have on the thermodynamics?
Associated with a transition state is a flat valley on the PES which connects two minima.
These transition state valleys will make a contribution to 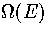 .
To consider their effect we need an expression for the density of states of a transition state valley.
.
To consider their effect we need an expression for the density of states of a transition state valley.
We write the partition function for the transition state valley as a product of a
vibrational partition function for the 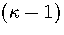 modes orthogonal to
the transition vector and a translational partition function for motion
along the transition state valley. This separation gives
modes orthogonal to
the transition vector and a translational partition function for motion
along the transition state valley. This separation gives
| 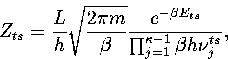 |
(3.12) |
where L is the length of the transition state valley.
Inverse Laplace transforming this expression gives for the density of states of the transition state valley,
| 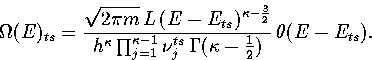 |
(3.13) |
Our expression for the total density of states is then
| 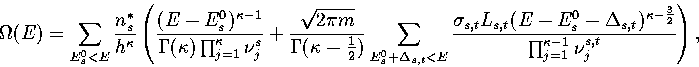 |
(3.14) |
where 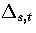 is the barrier height of transition state t from minimum s,
and the reaction path degeneracy
is the barrier height of transition state t from minimum s,
and the reaction path degeneracy 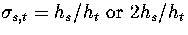 for
non-degenerate and degenerate rearrangement mechanisms, respectively[168].
A degenerate transition state connects
different permutational isomers of the same minimum.
In the
for
non-degenerate and degenerate rearrangement mechanisms, respectively[168].
A degenerate transition state connects
different permutational isomers of the same minimum.
In the 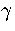 formulation we now have
formulation we now have
| 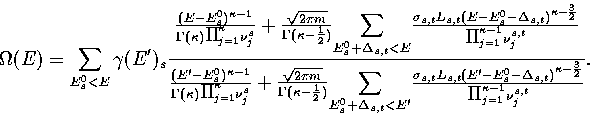 |
(3.15) |
Geometrically, the phase volume associated with the transition state valley is an elliptical hypercylinder.
There is also a term due to the phase space overlap of this hypercylinder with the hyperellipsoid
associated with the minimum.
It can be evaluated[169], however it is a small term and so we neglect it, especially as initially
we are only trying to determine the magnitude of the effect of the transition state valleys.
The set of transition states previously calculated is not an exhaustive set for the sample of minima. Its
incompleteness could cause an underestimation of the density of states arising from
the transition state valleys. We therefore performed a more exhaustive search
for transition states from 13 minima representing a wide range of
energies. This search indicated that a reasonable estimate of the average
number of low energy transition states per minimum was 20 (not counting permutational isomers).
For each minimum the density of states
of the known transition state valleys was multiplied by 20/ntss, where ntss is
the number of known transition states for minimum s. If the sample of
transition states contained none connected to a particular minimum, it was
assigned 20 transition states with the average barrier height and average
frequency. The length of the transition state valley was estimated using
| 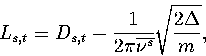 |
(3.16) |
where Ds,t is the displacement in configuration space between minimum s and transition state t,
and 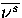 is the average normal mode frequency of s.
The second term is the average radius of the harmonic
well in configuration space at an energy
is the average normal mode frequency of s.
The second term is the average radius of the harmonic
well in configuration space at an energy 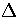 above the minimum.
above the minimum.
From the expression for 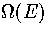 in equation 3.15
the temperature can be calculated using equation 3.10.
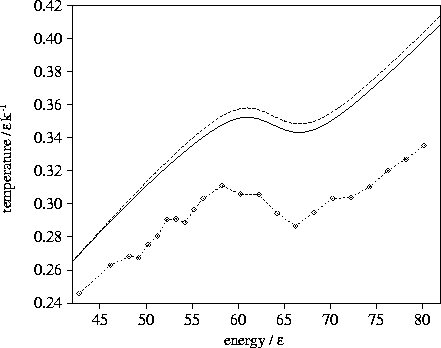
It can be seen from the microcanonical caloric curves given in Figure 3.6 that the
transition state valleys cause the caloric curve to bend away from the harmonic curve
and the Van der Waals loop to be displaced downwards, but these effects are small.
Even if the number of transition states connected to a minimum is assumed to
be greater than 20 the effects are only slightly increased.
The addition of the density of states of the
transition state valleys only accounts for a small part of the difference between
the harmonic and the true caloric curves. This result occurs not because the contribution of
the transition state valleys to the density of states is small compared to that of
the minima--in fact
the transition state valleys make a larger contribution than the minima above about
in equation 3.15
the temperature can be calculated using equation 3.10.
It can be seen from the microcanonical caloric curves given in Figure 3.6 that the
transition state valleys cause the caloric curve to bend away from the harmonic curve
and the Van der Waals loop to be displaced downwards, but these effects are small.
Even if the number of transition states connected to a minimum is assumed to
be greater than 20 the effects are only slightly increased.
The addition of the density of states of the
transition state valleys only accounts for a small part of the difference between
the harmonic and the true caloric curves. This result occurs not because the contribution of
the transition state valleys to the density of states is small compared to that of
the minima--in fact
the transition state valleys make a larger contribution than the minima above about
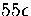 . Rather it occurs because the density of states for the transition
state valleys is not very different from that of the minima; the valleys are modelled as
harmonic in all but one dimension. We therefore conclude that a method of modelling the
anharmonicity of the wells on the PES is needed to obtain an accurate
. Rather it occurs because the density of states for the transition
state valleys is not very different from that of the minima; the valleys are modelled as
harmonic in all but one dimension. We therefore conclude that a method of modelling the
anharmonicity of the wells on the PES is needed to obtain an accurate 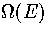 .This agrees with Stillinger and Stillinger's conclusion that intrawell anharmonicity
is dominant for LJ55 based on the fact that the caloric curve significantly deviates from the
harmonic form at energies where the cluster always resides in the icosahedral well[108].
.This agrees with Stillinger and Stillinger's conclusion that intrawell anharmonicity
is dominant for LJ55 based on the fact that the caloric curve significantly deviates from the
harmonic form at energies where the cluster always resides in the icosahedral well[108].
Figure 3.6:
Microcanonical caloric curves for LJ55 using the 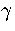 formula with (solid line)
and without (dashed line) the contribution from transition state valleys for sample A.
The calculated caloric curve is compared to simulation (dashed line with diamonds).
formula with (solid line)
and without (dashed line) the contribution from transition state valleys for sample A.
The calculated caloric curve is compared to simulation (dashed line with diamonds).
 |



Next: The effect of well
Up: Anharmonicity
Previous: Anharmonicity
Home: Return to my homepage
Jon Doye
8/27/1997
![]() modes orthogonal to
the transition vector and a translational partition function for motion
along the transition state valley. This separation gives
modes orthogonal to
the transition vector and a translational partition function for motion
along the transition state valley. This separation gives
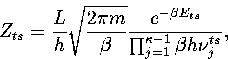
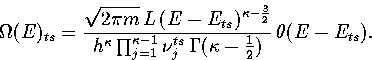
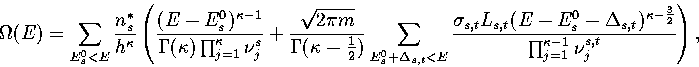
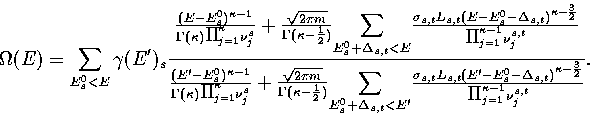
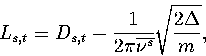
![]() in equation 3.15
the temperature can be calculated using equation 3.10.
It can be seen from the microcanonical caloric curves given in Figure 3.6 that the
transition state valleys cause the caloric curve to bend away from the harmonic curve
and the Van der Waals loop to be displaced downwards, but these effects are small.
Even if the number of transition states connected to a minimum is assumed to
be greater than 20 the effects are only slightly increased.
The addition of the density of states of the
transition state valleys only accounts for a small part of the difference between
the harmonic and the true caloric curves. This result occurs not because the contribution of
the transition state valleys to the density of states is small compared to that of
the minima--in fact
the transition state valleys make a larger contribution than the minima above about
in equation 3.15
the temperature can be calculated using equation 3.10.
It can be seen from the microcanonical caloric curves given in Figure 3.6 that the
transition state valleys cause the caloric curve to bend away from the harmonic curve
and the Van der Waals loop to be displaced downwards, but these effects are small.
Even if the number of transition states connected to a minimum is assumed to
be greater than 20 the effects are only slightly increased.
The addition of the density of states of the
transition state valleys only accounts for a small part of the difference between
the harmonic and the true caloric curves. This result occurs not because the contribution of
the transition state valleys to the density of states is small compared to that of
the minima--in fact
the transition state valleys make a larger contribution than the minima above about
![]() . Rather it occurs because the density of states for the transition
state valleys is not very different from that of the minima; the valleys are modelled as
harmonic in all but one dimension. We therefore conclude that a method of modelling the
anharmonicity of the wells on the PES is needed to obtain an accurate
. Rather it occurs because the density of states for the transition
state valleys is not very different from that of the minima; the valleys are modelled as
harmonic in all but one dimension. We therefore conclude that a method of modelling the
anharmonicity of the wells on the PES is needed to obtain an accurate ![]() .This agrees with Stillinger and Stillinger's conclusion that intrawell anharmonicity
is dominant for LJ55 based on the fact that the caloric curve significantly deviates from the
harmonic form at energies where the cluster always resides in the icosahedral well[108].
.This agrees with Stillinger and Stillinger's conclusion that intrawell anharmonicity
is dominant for LJ55 based on the fact that the caloric curve significantly deviates from the
harmonic form at energies where the cluster always resides in the icosahedral well[108].
