Barrier heights

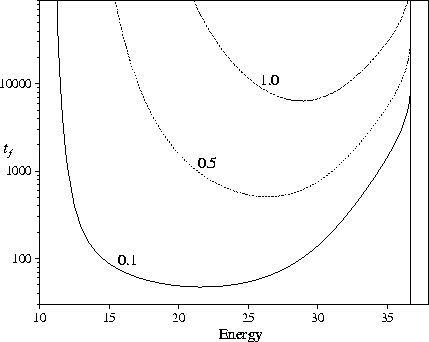
The first modification that we make is to change the barrier height. Unsurprisingly, increasing b leads to a reduction in the rate of relaxation to the global minimum (Figure 5.6). More interesting is the dependence of this effect upon the energy: increasing the barrier heights leads to a much larger increase in t_f at low energies. This is because a larger fraction of the kinetic energy must be converted to potential energy to overcome the barriers at low energies. The energy at which the maximum folding' rate occurs increases as the barrier heights increase. The shape of the minimum in t_f is also dependent on b, becoming broader as the barrier heights are decreased; at b=0.01 there is a larger energy window for which fast relaxation to the global minimum can occur.

  

Figure 5.6: The dependence of t_f on the barrier height, b, for our standard PES. t_f is defined by P₁(t_f)=0.8. The vertical dotted line denotes the energy at which P₁^eq=0.8. Each line is marked by the value of b.

Similar behaviour is observed for the canonical ensemble, namely the rate of relaxation to the global minimum has a $\exp(-\beta b)$ dependence on the barrier height. Therefore, at fixed temperature the relaxation rate has a rigorously exponential dependence on b, and changing b has a greater effect on the relaxation rate at low temperature.

These results can easily be understood in the language of Bryngelson and Wolynes[243,244,245]: increasing the barrier heights corresponds to increasing T_g without changing T_f, hence decreasing the ratio T_f/T_g and the folding' ability. Potassium chloride clusters provide a good example of systems for which relatively small barrier heights produce rapid relaxation down the PES[252].