|
Research
|
Global Optimization
Global optimization is the task of finding the lowest (or highest) value of a function. It is important for cluster science because the global minimum of the potential energy corresponds to the equilibrium structure at 0K (and is a good guide to the structure at other temperatures).The difficulty of this task arises from the exponential increase in the number of minima with size. Therefore, it is important to have as an efficient as possible algorithm if it is going to be possible to study large systems.
One approach to global optimization is to transform the potential energy surface to a form, for which optimization is hopefully easier. A transformation that we have found to be particularly useful is depicted below. Indeed it underlies all the global optimization algorithms that are most successful for clusters. The transformation involves associating the energy of a point in configuration space with the energy of the minimum that is obtained by performing a local optimization from that point.
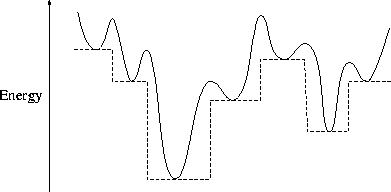
As can be seen the transformation turns the potential energy surface into a series of staircases. All downhill barriers are removed and the associated changes to the thermodynamics make overcoming barriers between funnels much easier. Therefore, relaxation downhill is faster and the effects of trapping are reduced, thus making global optimization much more efficient.
The large database of cluster structures that has been obtained by the application of this "basin-hopping" algorithm are accessible from the Cambridge Cluster Database.
Associated Publications
- J.P.K. Doye, Phys. Rev. E 62, 8753-8761 (2000)
The effect of compression on the global optimization of atomic clusters - R. H. Leary and J.P.K. Doye, Phys. Rev. E 60, R6320-R6322 (1999)
Tetrahedral global minimum for the 98-atom Lennard-Jones cluster - J.P.K. Doye, D.J. Wales and M.A. Miller, J. Chem. Phys. 109, 8143-8153 (1998)
Thermodynamics and the global optimization of Lennard-Jones clusters - J.P.K. Doye and D.J. Wales, Phys. Rev. Lett. 80, 1357-1360 (1998)
Thermodynamics of global optimization - D.J. Wales and J.P.K. Doye, J. Phys. Chem. A, 101, 5111-5116 (1997)
Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 Atoms -
J.P.K. Doye and D.J. Wales, Z. Phys. D, 40, 194-197 (1997)
Traversing the potential energy surface by eigenvector-following: applications to global optimisation and the structural transformations of clusters