Lennard-Jones Clusters

The structural, thermodynamic and dynamic properites of Lennard-Jones clusters have been much studied, making them an ideal system to explore systematically how disconnectivity graphs evolve with size. There are two types of size effects. Firstly, those due to the exponential increase in the number of minima with size. Secondly, on top of this are size-specific effects, where the topography of the energy landscape has a particular form.

The clusters we consider are LJ₁₃, LJ₁₉, LJ₃₁, LJ₃₈, LJ₅₅ and LJ₇₅

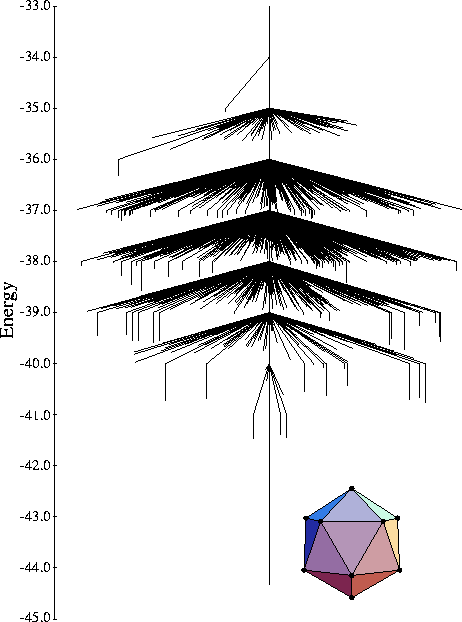
LJ₁₃

All 1467 minima from a near-exhaustive search of the landscape are depicted in this graph. This size is a magic number because it is possible to form a complete icosahedron, which is the global minimum. All the minima are within three rearrangements of the icosahedron, and the energy rises with distance from the global minimum. The landscape is a good funnel allowing efficient relaxation to the icosahedron from the high-energy states.

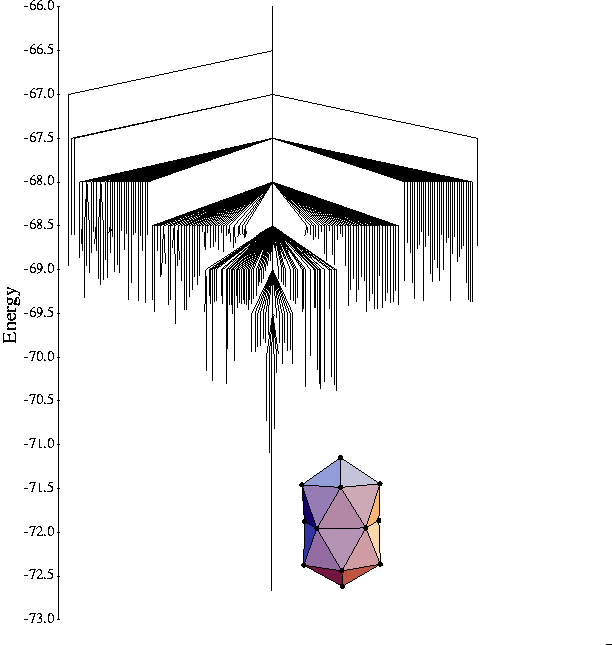
LJ₁₉

For this and the larger clusters, it is impossible to obtain a complete catalogue of the minima, therefore the seach of the energy landscape is concentrated on the low energy minima, and only the 200 lowest-energy minima are included in the graph. The global minimum is the double icosahedron, which represents a sub-shell closing for an overlayer on the 13-atom icosahedron. Like LJ₁₃ the energy landscape is a single funnel but with a shallower gradient towards the global minimum.

LJ₃₁

For this cluster there are two competing types of overlayer. The global minimum has a Mackay overlayer, whereas the second lowest-energy minimum has an anti-Mackay overlayer. The low energetic bias towards the global minimum and the large barriers between the low-energy minima frustrate relaxation towards the global minimum.

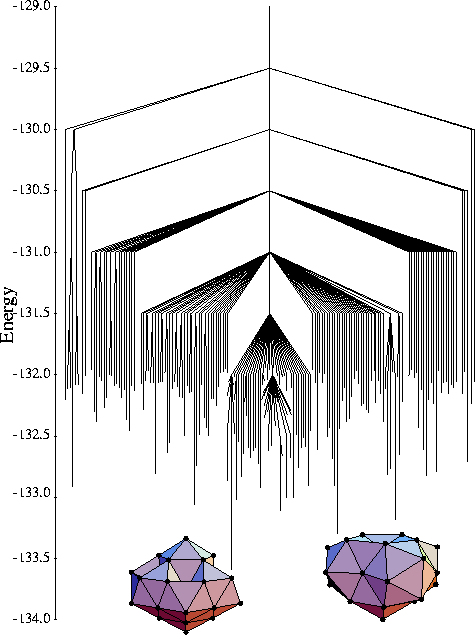
LJ₃₈

This system has an archetypal double funnel. Funnels are associated with the two lowest-energy minima. The global minimum is a face-centred-cubic truncated octahedron, whereeas the second lowest-energy minimum is icosahedral. Furthermore, there are many more minima associated with the icosahedral funnel, Therefore, relaxation from high energy states is much more likely to lead to the icosahedral funnel due to this greater width. Subsequent, equilibration between the funnels is slow due to the large barriers between them.

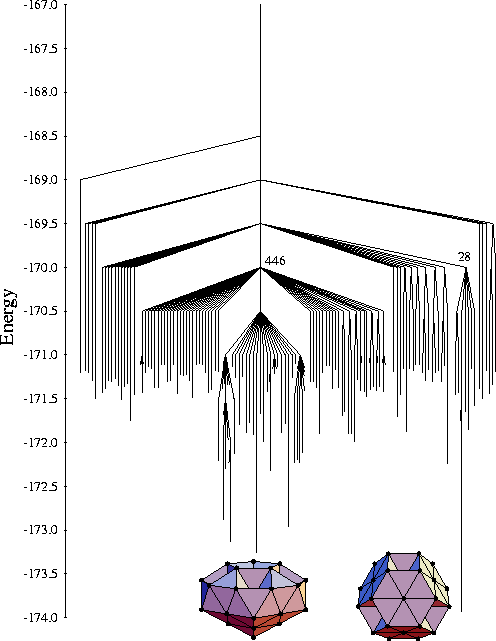
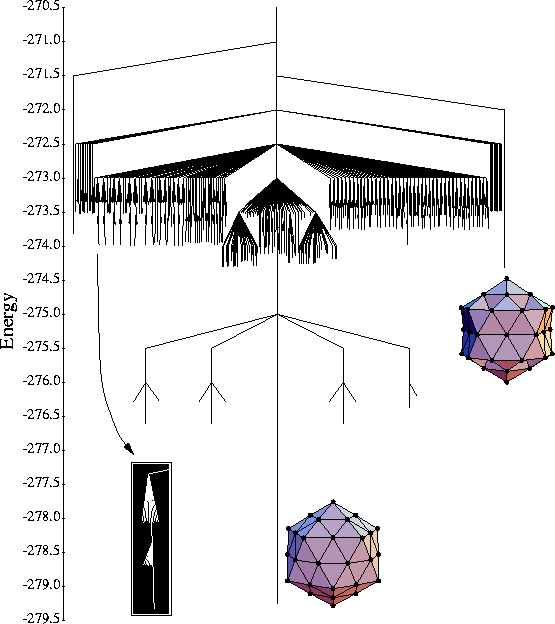
LJ₅₅

This size is also a magic number with a pronounced global minimum - the complete Mackay icosahedron - and a single-funnel landscape. The graph only provides a picture of the bottom of the energy landscape with the two bands of minima corresponding to Mackay icosahedra with one and two defects. These separate into families of structures as illustrated by the inset. Also illustrated is a high-symmetry minimum which is separated from the global minimum by a high-barrier twist rearrangement.

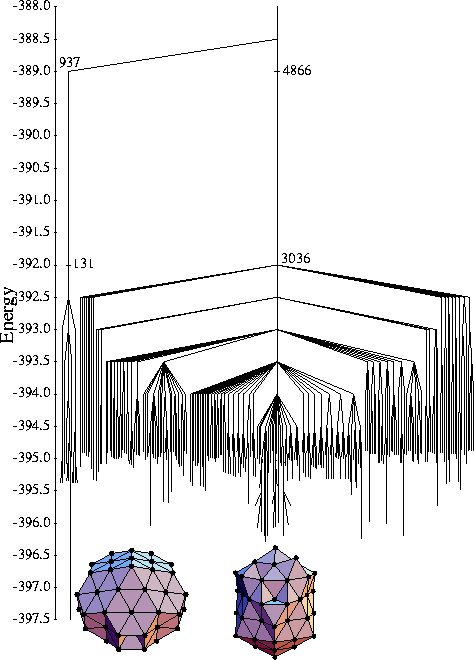
LJ₇₅

This cluster also has a double-funnel landscape, again associated with two competing types of structure. The global minimum is a Marks decahedron, whereas most of the other low-energy minima are icosahedral. As with LJ₃₈ this causes the system to enter the wider icosahedral on relaxation from high energy.

Associated Publications

• J.P.K. Doye, M.A. Miller and D.J. Wales, J. Chem. Phys. 111, 8417-8428 (1999)

Evolution of the Potential Energy Surface with Size for Lennard-Jones Clusters