Energy Landscapes

The multi-dimensionality of the energy landscape makes it hard to visualize what the energy landscape `looks like'. Disconnectivity graphs are a useful way of overcoming this problem. They provide a picture of the magnitudes of the barriers between minima and enable large scale topographical features, such as funnels, to be visualized. A collection of disconnectivity graphs can be found here.

The thermodynamic properties of a system are given by the partition function. As this can be rewritten as a sum over all the minima of the partition functions of each individual minimum, we are able to compute the thermodynamic properties of a system from a representative sample of minima. This enables the thermodynamic contributions of different regions of the energy landscape to be examined, thus providing physical insight.

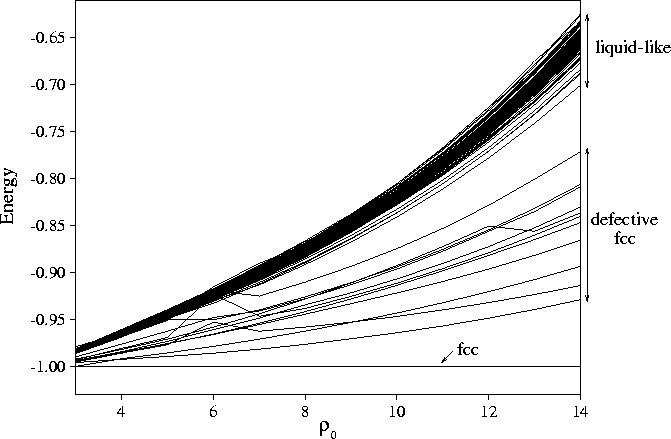
For example, the energy landscape picture of melting is of a transition from the global minimum (and perhaps other low energy minima based upon it) to the huge number of high energy minima associated with the liquid because of their greater entropy. One of the determinants of the melting point is the energy gap between the global minimum and the `liquid-like' minima; if this gap increases the liquid phase is destabilized. Much interest in the effect of the interaction range on the phase diagram has been generated by the discovery that a liquid of C₆₀ molecules is only marginally stable. This unusual behaviour was attributed to the short range of the interactions between these molecules (relative to their size). I was able to provide a structural explanation for this behaviour by following the energetics of a set of minima as function of a parameter, rho, which determines the range of the interactions. The energy gap between the solid and the liquid-like minima increase as the range of the potential is decreased (see picture below). The potential well becomes increasingly narrow as the range decreases giving rise to an increasing energetic penalty for the dispersion of nearest-neighbour distances associated with the disordered liquid-like minima.