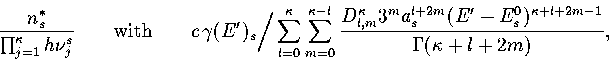


Next: The Structure and Stability
Up: Thermodynamics of Small Lennard-Jones
Previous: Thermodynamic Properties
Home: Return to my homepage
Here, building upon previous work[134], we consider the conditions for
a Van der Waals loop to occur in the microcanonical caloric curve using a two state model.
By differentiating equation 3.30, we obtain
| ![\begin{displaymath}
\left({\partial T \over \partial E} \right)_{N,V} =
T^2 \su...
...} \left({\partial p_i \over \partial E} \right)_{N,V} \right], \end{displaymath}](img197.gif) |
(3.50) |
where the probabilities and their derivatives obey  and
and 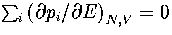 .For a two state system, this expression becomes
.For a two state system, this expression becomes
| 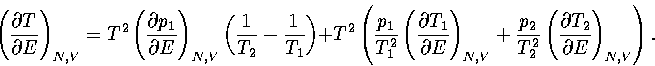 |
(3.51) |
The first term in this expression is negative and the second positive
(assuming region 1 has a lower potential energy than region 2).
To exhibit a Van der Waals loop, the caloric curve must have a region of negative slope,
and therefore the following inequality must be satisfied for some range of energy,
| 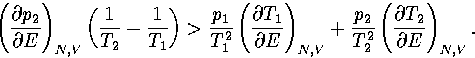 |
(3.52) |
If we assume both regions behave harmonically, then 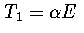 and
and
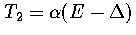 , where
, where 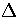 is the potential energy difference
between the minima of the two regions.
This assumption gives
is the potential energy difference
between the minima of the two regions.
This assumption gives

(3.53)
(3.54)
In the middle of the coexistence region where p1=p2=1/2, neglecting second order terms in  gives
gives
| 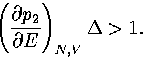 |
(3.55) |
This equation was previously derived by Bixon and Jortner[152]
for Van der Waals loops in the kinetic temperature.
We now continue the analysis, first noting that
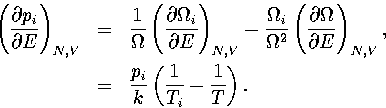
(3.56)
(3.57)
Therefore, using equation 3.30
| 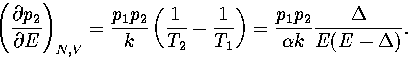 |
(3.58) |
Substituting this result into equation 3.53 and rearranging gives
| 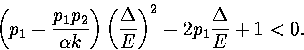 |
(3.59) |
Taking the middle of the coexistence region, where p1=p2=1/2 and
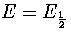 :
:
| 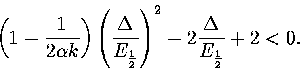 |
(3.60) |
As this quadratic has negative curvature for all realistic values of 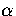 ,the above inequality has a physically meaningful solution when
,the above inequality has a physically meaningful solution when 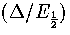 is greater than
the larger root of the quadratic. This solution is
is greater than
the larger root of the quadratic. This solution is
| 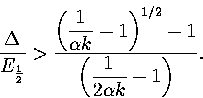 |
(3.61) |
For a single harmonic minimum of an N-atom cluster
| 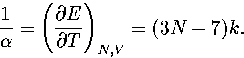 |
(3.62) |
Hence,
| 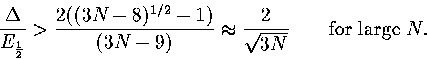 |
(3.63) |
A similar relationship can be derived for the N-dependence of Van der Waals loops in the caloric curve of
the isopotential ensemble. In this case
| 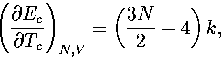 |
(3.64) |
where Ec is the potential energy and Tc is the isopotential temperature.
Hence,
| 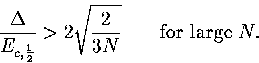 |
(3.65) |
As 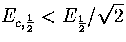 , this confirms that a Van der Waals loop is more likely
in the isopotential ensemble than the microcanonical ensemble.
As we saw earlier, 13 has a Van der Waals loop in the isopotential caloric curve
but not in the microcanonical curve.
, this confirms that a Van der Waals loop is more likely
in the isopotential ensemble than the microcanonical ensemble.
As we saw earlier, 13 has a Van der Waals loop in the isopotential caloric curve
but not in the microcanonical curve.
From equation 3.63 it is clear that for a series of structures with similar values of
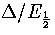 , a Van der Waals loop will become more likely as the size increases (Figure 3.16).
This result is in good agreement with simulations of icosahedral
LJ[135] and cuboctahedral gold clusters[136].
, a Van der Waals loop will become more likely as the size increases (Figure 3.16).
This result is in good agreement with simulations of icosahedral
LJ[135] and cuboctahedral gold clusters[136].
Figure 3.16:
Plots of temperature (top) and probability, p2, (bottom) for a two state system.
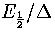 is kept constant as N is varied.
The solid line is for small N, long dashed line is for intermediate N
and the short dashed line for the bulk limit.
is kept constant as N is varied.
The solid line is for small N, long dashed line is for intermediate N
and the short dashed line for the bulk limit.
 |
In the bulk limit the above model predicts the caloric curve will be vertical at  (Figure 3.16), which is clearly at variance with the expected behaviour
for a bulk first-order phase transition.
This discrepancy arises because we have not allowed for the cluster dividing into distinct
solid-like and liquid-like regions, which would contribute a term of the form
(Figure 3.16), which is clearly at variance with the expected behaviour
for a bulk first-order phase transition.
This discrepancy arises because we have not allowed for the cluster dividing into distinct
solid-like and liquid-like regions, which would contribute a term of the form
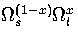 to the density of states,
where x is the fraction of the cluster that is liquid-like.
Such phase separation does not occur for small clusters because the energy of the dividing
surface makes it unfavourable, but for the bulk the interface is a negligible fraction of the total energy.
Recently, an analytical model has been investigated which predicts the size evolution of the
microcanonical caloric curve as phase separation becomes possible[176].
to the density of states,
where x is the fraction of the cluster that is liquid-like.
Such phase separation does not occur for small clusters because the energy of the dividing
surface makes it unfavourable, but for the bulk the interface is a negligible fraction of the total energy.
Recently, an analytical model has been investigated which predicts the size evolution of the
microcanonical caloric curve as phase separation becomes possible[176].
Equation 3.63 also shows us that a Van der Waals loop becomes
more likely as the quantity 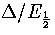 increases.
We can understand the conditions for this quantity to be large by considering the density of states for each region.
For simplicity we do this within the harmonic approximation. We consider
region 1 to be made up of n1 similar geometric isomers (with the same
energy, vibrational frequencies and point group), and region 2 of n2.
Each geometric isomer has 2N!/hi permutational isomers.
These assumptions yield
increases.
We can understand the conditions for this quantity to be large by considering the density of states for each region.
For simplicity we do this within the harmonic approximation. We consider
region 1 to be made up of n1 similar geometric isomers (with the same
energy, vibrational frequencies and point group), and region 2 of n2.
Each geometric isomer has 2N!/hi permutational isomers.
These assumptions yield
| 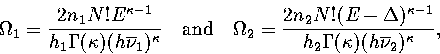 |
(3.66) |
where hi is the order of the point group for states in region i.
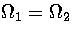 at
at 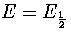 . Hence,
. Hence,
| 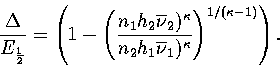 |
(3.67) |
From this expression we can see that 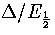 increases, making a Van der Waals loop more likely,
as region 1 becomes more solid-like (a few high symmetry, rigid states) and as region 2 becomes
more liquid-like (many low symmetry, non-rigid states).
increases, making a Van der Waals loop more likely,
as region 1 becomes more solid-like (a few high symmetry, rigid states) and as region 2 becomes
more liquid-like (many low symmetry, non-rigid states).
Appendix: Thermodynamic Formulae
APPENDIX: THERMODYNAMIC FORMULAE
In this appendix, the formulae for some of the thermodynamic quantities
that can be calculated by the superposition method are given.
The thermodynamic functions are derived from the following definitions.
In the isopotential ensemble,
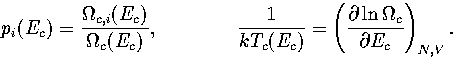
In the microcanonical ensemble,
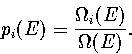
In the canonical ensemble,
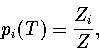
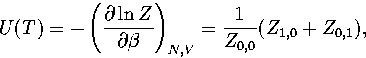
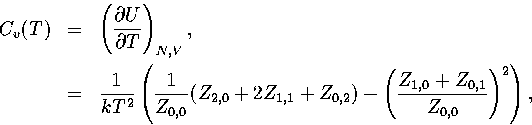
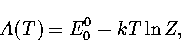
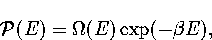

where in 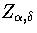 the derivative of the exponential function of
the derivative of the exponential function of  in Z has been taken
in Z has been taken 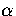 times and the derivative of the inverse power of
times and the derivative of the inverse power of
 in Z
in Z 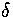 times. Therefore, Z=Z0,0.
times. Therefore, Z=Z0,0.
Below, we give the thermodynamic functions for the 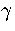 formulation with
a first-order anharmonic correction which was used for 55.
formulation with
a first-order anharmonic correction which was used for 55.
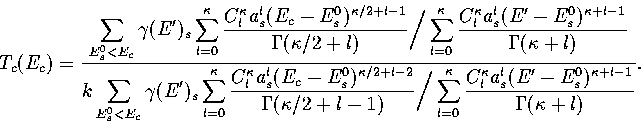
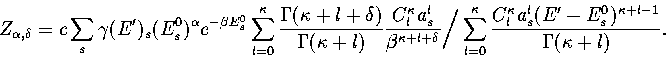
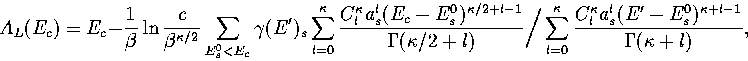
where
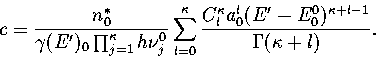
The harmonic forms can be recovered by taking the l=0 term. We
obtain the n* formulation by replacing
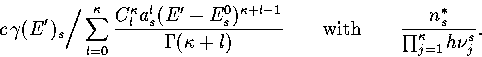
Below, we give the thermodynamic functions
for the n* formulation with second-order
anharmonic corrections which was used for 13.
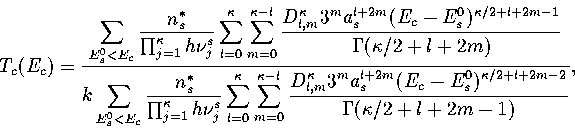
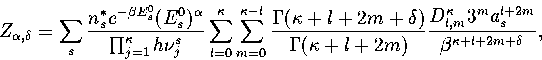
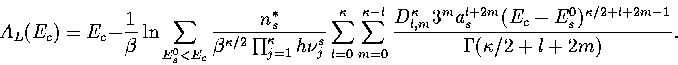
The harmonic forms can be recovered by taking the l=0, m=0 term,
and the first-order correction forms by taking the m=0 terms.
We obtain the 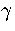 formulation by replacing
formulation by replacing
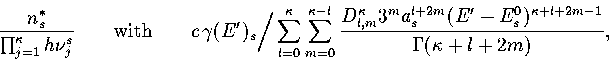
where




Next: The Structure and Stability
Up: Thermodynamics of Small Lennard-Jones
Previous: Thermodynamic Properties
Home: Return to my homepage
Jon Doye
8/27/1997
![\begin{displaymath}
\left({\partial T \over \partial E} \right)_{N,V} =
T^2 \su...
...} \left({\partial p_i \over \partial E} \right)_{N,V} \right], \end{displaymath}](img197.gif)
![\begin{displaymath}
\left({\partial T \over \partial E} \right)_{N,V} =
T^2 \su...
...} \left({\partial p_i \over \partial E} \right)_{N,V} \right], \end{displaymath}](img197.gif)
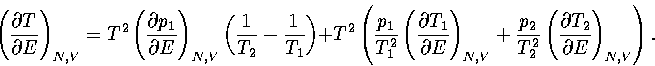
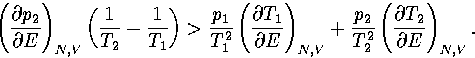
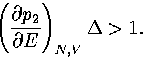
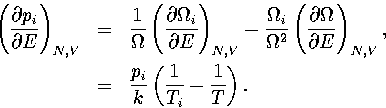
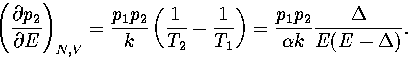
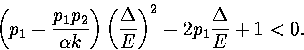
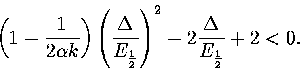
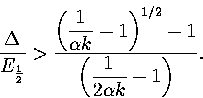
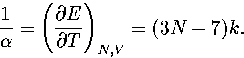
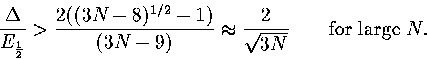
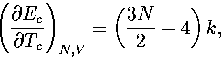
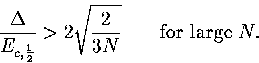
![]() , a Van der Waals loop will become more likely as the size increases (Figure 3.16).
This result is in good agreement with simulations of icosahedral
LJ[135] and cuboctahedral gold clusters[136].
, a Van der Waals loop will become more likely as the size increases (Figure 3.16).
This result is in good agreement with simulations of icosahedral
LJ[135] and cuboctahedral gold clusters[136].

![]() (Figure 3.16), which is clearly at variance with the expected behaviour
for a bulk first-order phase transition.
This discrepancy arises because we have not allowed for the cluster dividing into distinct
solid-like and liquid-like regions, which would contribute a term of the form
(Figure 3.16), which is clearly at variance with the expected behaviour
for a bulk first-order phase transition.
This discrepancy arises because we have not allowed for the cluster dividing into distinct
solid-like and liquid-like regions, which would contribute a term of the form
![]() to the density of states,
where x is the fraction of the cluster that is liquid-like.
Such phase separation does not occur for small clusters because the energy of the dividing
surface makes it unfavourable, but for the bulk the interface is a negligible fraction of the total energy.
Recently, an analytical model has been investigated which predicts the size evolution of the
microcanonical caloric curve as phase separation becomes possible[176].
to the density of states,
where x is the fraction of the cluster that is liquid-like.
Such phase separation does not occur for small clusters because the energy of the dividing
surface makes it unfavourable, but for the bulk the interface is a negligible fraction of the total energy.
Recently, an analytical model has been investigated which predicts the size evolution of the
microcanonical caloric curve as phase separation becomes possible[176].
![]() increases.
We can understand the conditions for this quantity to be large by considering the density of states for each region.
For simplicity we do this within the harmonic approximation. We consider
region 1 to be made up of n1 similar geometric isomers (with the same
energy, vibrational frequencies and point group), and region 2 of n2.
Each geometric isomer has 2N!/hi permutational isomers.
These assumptions yield
increases.
We can understand the conditions for this quantity to be large by considering the density of states for each region.
For simplicity we do this within the harmonic approximation. We consider
region 1 to be made up of n1 similar geometric isomers (with the same
energy, vibrational frequencies and point group), and region 2 of n2.
Each geometric isomer has 2N!/hi permutational isomers.
These assumptions yield
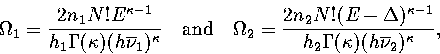
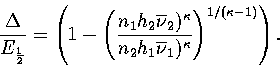
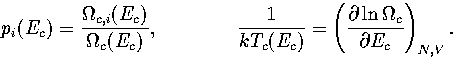
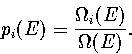
![]()
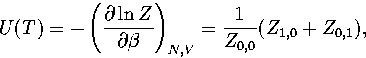
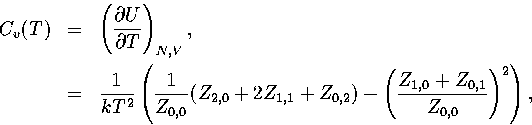
![]()
![]()
![]()
![]() formulation with
a first-order anharmonic correction which was used for 55.
formulation with
a first-order anharmonic correction which was used for 55.
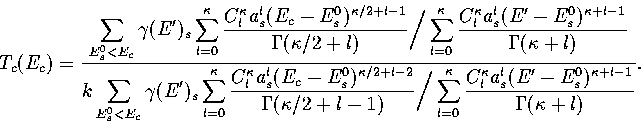
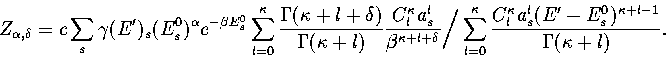
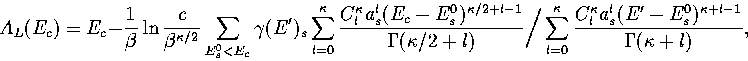
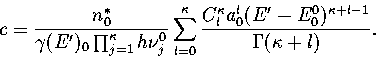
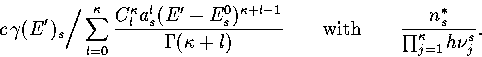
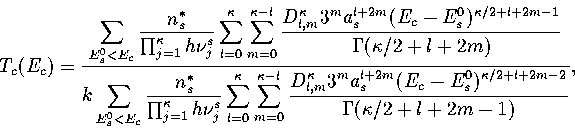
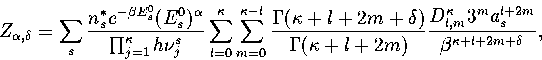
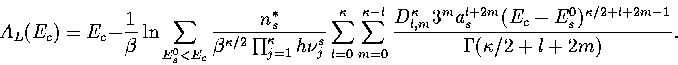
![]() formulation by replacing
formulation by replacing