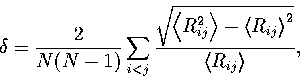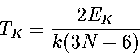


Next: The 55-atom Lennard-Jones Cluster
Up: Thermodynamics of Small Lennard-Jones
Previous: Introduction
Home: Return to my homepage
The potential used in this study was the Lennard-Jones form[83],
| ![\begin{displaymath}
E = 4\,\epsilon\sum_{i<j}\left[\left(\sigma\over r_{ij}\right)^{12}-\left(\sigma\over r_{ij}\right)^6\right],\end{displaymath}](img80.gif) |
(3.1) |
where rij is the distance between atoms i and j.
With  ,
,  and m as the units of energy, distance and mass, respectively,
the unit of time is
and m as the units of energy, distance and mass, respectively,
the unit of time is  .
MD simulations of the microcanonical ensemble were conducted using the
velocity Verlet algorithm[156].
The initial phase point had zero linear and angular momentum.
To prevent evaporation the clusters were placed in a container with walls
represented by a LJ type repulsion[153,157].
When an atom hit the wall of the container an equal and opposite force was exerted on
the rest of the cluster to prevent linear momentum transfer.
As the two forces are collinear, there is also no transfer of angular momentum.
The effect of the box is to restrict the phase space considered to bound clusters.
The time step used was 0.0465 reduced time units,
which is equivalent to
.
MD simulations of the microcanonical ensemble were conducted using the
velocity Verlet algorithm[156].
The initial phase point had zero linear and angular momentum.
To prevent evaporation the clusters were placed in a container with walls
represented by a LJ type repulsion[153,157].
When an atom hit the wall of the container an equal and opposite force was exerted on
the rest of the cluster to prevent linear momentum transfer.
As the two forces are collinear, there is also no transfer of angular momentum.
The effect of the box is to restrict the phase space considered to bound clusters.
The time step used was 0.0465 reduced time units,
which is equivalent to  s for Ar.
s for Ar.
The relative root-mean-square interatomic separation 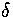 was used to assess the degree of melting.
It is defined as
was used to assess the degree of melting.
It is defined as
| 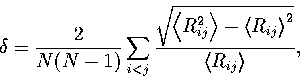 |
(3.2) |
where the angle brackets indicate that an
average is taken over the whole trajectory. Lindemann's criterion[158]
states that melting is expected when 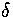 becomes greater than about 0.1.
becomes greater than about 0.1.
The kinetic temperature is calculated from the kinetic energy, EK, via the generalized equipartition theorem:
| 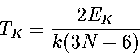 |
(3.3) |
by taking the mean of TK over the whole trajectory.
This expression is exact in the canonical ensemble, but TK differs by 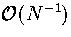 from the thermodynamic definition of temperature (equation 3.10)
in the microcanonical ensemble[159].
STA temperatures were found by averaging TK over 500 time steps.
from the thermodynamic definition of temperature (equation 3.10)
in the microcanonical ensemble[159].
STA temperatures were found by averaging TK over 500 time steps.



Next: The 55-atom Lennard-Jones Cluster
Up: Thermodynamics of Small Lennard-Jones
Previous: Introduction
Home: Return to my homepage
Jon Doye
8/27/1997
![\begin{displaymath}
E = 4\,\epsilon\sum_{i<j}\left[\left(\sigma\over r_{ij}\right)^{12}-\left(\sigma\over r_{ij}\right)^6\right],\end{displaymath}](img80.gif)
![\begin{displaymath}
E = 4\,\epsilon\sum_{i<j}\left[\left(\sigma\over r_{ij}\right)^{12}-\left(\sigma\over r_{ij}\right)^6\right],\end{displaymath}](img80.gif)
![]() was used to assess the degree of melting.
It is defined as
was used to assess the degree of melting.
It is defined as