Complex Networks and Energy Landscapes

As the size of a system increases, the potential energy surface (or energy landscape) rapidly becomes a very complex object. One way to gain insight into the underlying structure of this landscape is to analyse the topology of the network of minima that are connected by transition states. We have discovered that, like many social (e.g. the world-wide web, scientific collaborations, and even sexual contacts) and biochemical (e.g. protein-protein interactions, metabolic pathways) networks, the energy landscape is both a 'small world' and is 'scale-free'. Despite the complexity, any two minima are only a few steps away from each other, because the low-energy minima act as highly-connected hubs that mediate the shortest paths.

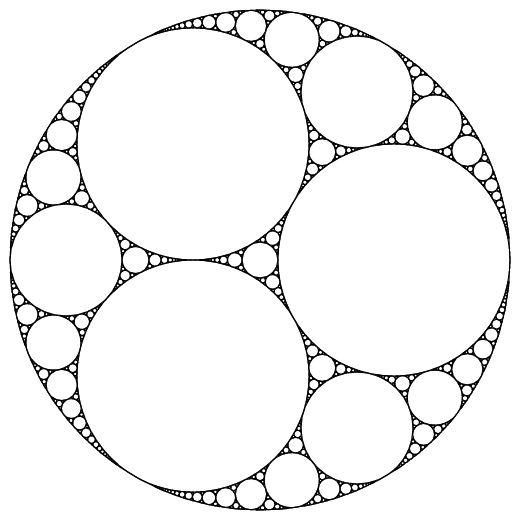We have also shown that the scale-free character of these networks reflects the nature of the division of the energy landscape into basins of attraction, which are hierarchical and seemingly fractal. Intriguingly, there are strong analogies to the way that space is tiled by hyperspheres in an Apollonian packing (a 2D-example is depicted right).

Projects in this area will explore the origins of these features of potential energy landscapes, and the consequences for the dynamics on such landscapes.

There is also the possibility of doing a networks project in collaboration with Mason Porter in Maths on social networks.

• C.P. Massen and J.P.K. Doye, J. Chem. Phys. 127, 114306 (2007)
  Preferential attachment during the evolution of a potential energy landscape
• C.P. Massen, J.P.K. Doye and R.W. Nash, Physica A 382, 683-692 (2007)
  Exploring the origins of the power-law properties of energy landscapes: An egg-box model
• C.P. Massen and J.P.K. Doye, Phys. Rev. E 75, 037101 (2007)
  Power-law distributions for the areas of the basins of attraction on a potential energy landscape
• C.P. Massen and J.P.K. Doye, Physica A 377, 351-362 (2007)
  A self-consistent approach to measure preferential attachment in networks and its application to an inherent structure network
• C.P. Massen and J.P.K. Doye, Phys. Rev. E, 71, 046101 (2005)
  Identifying "communities" within energy landscapes
• J.P.K. Doye and C.P. Massen, J. Chem. Phys. 122, 084105 (2005)
  Characterizing the network topology of the energy landscapes of atomic clusters
• J.P.K. Doye and C.P. Massen, Phys. Rev. E 71, 016128 (2005)
  Space-filling disk packings as model spatial scale-free networks
• J.P.K. Doye, Phys. Rev. Lett. 88, 238701 (2002)
  The network topology of a potential energy landscape: A static scale-free networ k