The Morse Potential
The Morse potential has the form:
The Morse potential may be written as
| 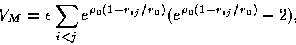 |
(1) |
where 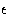 is the pair well depth and r0 the equilibrium pair separation.
In reduced units (
is the pair well depth and r0 the equilibrium pair separation.
In reduced units (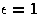 and r0=1) there is a single adjustable parameter,
and r0=1) there is a single adjustable parameter, 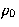 ,
which determines the range of the interparticle forces.
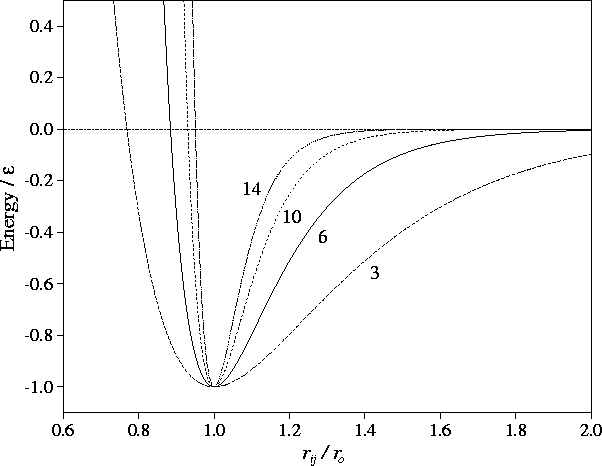
The Figure shows that decreasing
,
which determines the range of the interparticle forces.
The Figure shows that decreasing 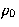 increases the range of the
attractive part of the potential and softens the repulsive wall, thus widening the
potential well.
The LJ potential
has the same curvature at the bottom of the well as the Morse potential when
increases the range of the
attractive part of the potential and softens the repulsive wall, thus widening the
potential well.
The LJ potential
has the same curvature at the bottom of the well as the Morse potential when  .
Girifalco has obtained an intermolecular potential for
.
Girifalco has obtained an intermolecular potential for
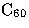 molecules
which is isotropic and short-ranged relative to the equilibrium pair separation,
with an effective value of
molecules
which is isotropic and short-ranged relative to the equilibrium pair separation,
with an effective value of 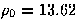 .
The alkali metals have longer-ranged interactions, for example
.
The alkali metals have longer-ranged interactions, for example
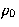 =3.15 has been suggested for sodium.
Fitting to bulk data gives a value of
=3.15 has been suggested for sodium.
Fitting to bulk data gives a value of 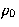 =3.96 for nickel.
=3.96 for nickel.
Figure:
The Morse potential for different values of the range parameter 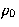 as indicated.
as indicated.
 |
Reference: P. M. Morse, Phys. Rev.34, 57 (1929).
Jon Doye
11/5/1997
